题目内容
在函数y=
(a为常数)的图象上三点(-1,y1),(-
,y2),(
,y3),则函数值y1、y2、y3的大小关系是 .
| -a2-1 |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
考点:反比例函数图象上点的坐标特征
专题:
分析:先根据反比例函数中k=a2+1>0判断出函数图象所在的象限,再根据各点横坐标的特点即可得出结论.
解答:解:∵在函数y=
(a为常数)中k=-a2-1<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵-<-
<0,
∴0<y1<y2.
∵
>0,
∴y3<0,
∴y3<y1<y2.
故答案为y3<y1<y2.
| -a2-1 |
| x |
∴函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵-<-
| 1 |
| 4 |
∴0<y1<y2.
∵
| 1 |
| 2 |
∴y3<0,
∴y3<y1<y2.
故答案为y3<y1<y2.
点评:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.

练习册系列答案
相关题目
 如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.
如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由. 如图,∠1,∠2,∠3,∠4,∠5,∠6中有
如图,∠1,∠2,∠3,∠4,∠5,∠6中有 如图,在△ABC的边CA、BA的延长线上分别取点D、E,连接DE,作∠E、∠C的平分线,交于点F.求证:∠F=
如图,在△ABC的边CA、BA的延长线上分别取点D、E,连接DE,作∠E、∠C的平分线,交于点F.求证:∠F= 如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证:
如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证: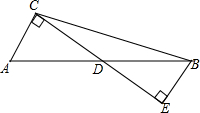 如图,D是AB的中点,CE过点D且AC⊥CE于C,BE⊥CE于E,已知sin∠BCD=
如图,D是AB的中点,CE过点D且AC⊥CE于C,BE⊥CE于E,已知sin∠BCD= 该几何体最少由多少个小立方体组成?最多由多少个小立方体组成.
该几何体最少由多少个小立方体组成?最多由多少个小立方体组成. 如图,有一艘油轮在海上的A处遇险,立即向救援基地C发出通知.救援基地发现有一艘救援船在B处,距离A处最近,于是通知B处的救援船迅速赶往A处营救.已知C在A的东南方向,且BA=20 nmile,AC=99 nmile,BC=101 nmile,请确定救援船前进的方向.
如图,有一艘油轮在海上的A处遇险,立即向救援基地C发出通知.救援基地发现有一艘救援船在B处,距离A处最近,于是通知B处的救援船迅速赶往A处营救.已知C在A的东南方向,且BA=20 nmile,AC=99 nmile,BC=101 nmile,请确定救援船前进的方向.