题目内容
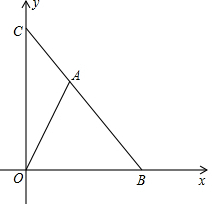 如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.
如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.(1)求BC所在直线的解析式.
(2)设点A的坐标为(x,y),△AOB的面积为S.求S关于x的函数解析式,并写出x的取值范围.
(3)当S=8时,求点A的坐标.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:计算题
分析:(1)设直线BC解析式为y=kx+b,把B与C坐标代入求出k与b的值,确定出直线BC解析式;
(2)三角形AOB以OB为底边,A纵坐标为高,表示出面积S,整理得到S关于x的解析式,求出x的范围即可;
(3)令S=8求出x的值,进而求出y的值,确定出A的坐标即可.
(2)三角形AOB以OB为底边,A纵坐标为高,表示出面积S,整理得到S关于x的解析式,求出x的范围即可;
(3)令S=8求出x的值,进而求出y的值,确定出A的坐标即可.
解答:解:(1)设直线BC解析式为y=kx+b,
把B(4,0)与C(0,4)代入得:
,
解得:k=-1,b=4,
则直线BC解析式为y=-x+4;
(2)根据题意得:S=
×4y=2y=2(-x+4)=-2x+8(0<x<4);
(3)令S=8,得到-2x+8=8,解得:x=0,y=4.
此时A(0,4).
把B(4,0)与C(0,4)代入得:
|
解得:k=-1,b=4,
则直线BC解析式为y=-x+4;
(2)根据题意得:S=
| 1 |
| 2 |
(3)令S=8,得到-2x+8=8,解得:x=0,y=4.
此时A(0,4).
点评:此题考查了待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 如图,△ABC内接于⊙O,直线CT切⊙O于点C,若∠AOB=80°,则∠BCA=
如图,△ABC内接于⊙O,直线CT切⊙O于点C,若∠AOB=80°,则∠BCA=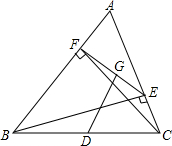 BE、CF为△ABC的二高,D为BC中点,BG⊥EF,求证:
BE、CF为△ABC的二高,D为BC中点,BG⊥EF,求证: 如图,有一艘油轮在海上的A处遇险,立即向救援基地C发出通知.救援基地发现有一艘救援船在B处,距离A处最近,于是通知B处的救援船迅速赶往A处营救.已知C在A的东南方向,且BA=20 nmile,AC=99 nmile,BC=101 nmile,请确定救援船前进的方向.
如图,有一艘油轮在海上的A处遇险,立即向救援基地C发出通知.救援基地发现有一艘救援船在B处,距离A处最近,于是通知B处的救援船迅速赶往A处营救.已知C在A的东南方向,且BA=20 nmile,AC=99 nmile,BC=101 nmile,请确定救援船前进的方向.