题目内容
20.现有6个质地,大小完全相同的小球上分别标有数字-1,0.5,$\frac{2}{3}$,1$\frac{1}{2}$,1,2.先将标有数字-1,0.5,1$\frac{1}{2}$的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里,现分别从这两个盒子里各随机取出一个小球,则取出的两个小球上的数字互为倒数的概率为$\frac{2}{9}$.分析 根据题意可以写出所有的可能性,从而可以得到取出的两个小球上的数字互为倒数的概率.
解答 解:由题意可得,所有的可能性为:
(-1,$\frac{2}{3}$)、(-1,1)、(-1,2)、
(0.5,$\frac{2}{3}$)、(0.5,1)、(0.5,2)、
(1$\frac{1}{2}$,$\frac{2}{3}$)、(1$\frac{1}{2}$,1)、(1$\frac{1}{2}$,2),
故取出的两个小球上的数字互为倒数的概率为:$\frac{2}{9}$,
故答案为:$\frac{2}{9}$.
点评 本题考查列表法与树状图法,解题的关键是明确题意,可以写出所有的可能性.

练习册系列答案
相关题目
11.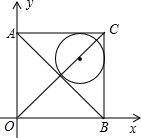 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 2$\sqrt{2}$ |
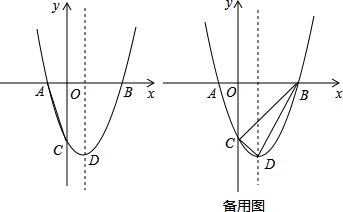
8.关于反比例函数y=-$\frac{4}{x}$,下列说法正确的是( )
| A. | 图象在第一、三象限 | B. | 图象经过点(2,-8) | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
15.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | “直角三角形三条边中垂线的交点是斜边的中点”这是必然事件 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”表示明天有半天都在降雨 | |
| D. | 了解一批电视机的使用寿命,适合用普查的方法 |
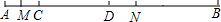 如图,已知线段AB=14,在AB上有C,D,M,N四点,且满足AC:CD:DB=1:2:4,AC=2AM,DB=4DN.求:MN的长度.
如图,已知线段AB=14,在AB上有C,D,M,N四点,且满足AC:CD:DB=1:2:4,AC=2AM,DB=4DN.求:MN的长度.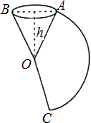 如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).
如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).