题目内容
14.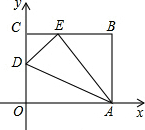 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )| A. | y=$\frac{3}{4}$x+5 | B. | y=$\frac{2}{5}$x+5 | C. | y=$\frac{1}{4}$x+5 | D. | y=$\frac{4}{5}$x+5 |
分析 首先在RT△ABE中,求出EB,再在RT△CDE中利用勾股定理即可解决问题.
解答 解: ∵△ADE是由△ADO翻折,
∵△ADE是由△ADO翻折,
∴DE=DO,AO=AE=10,
∵四边形OABC是矩形,
∴OC=AB=8,AO=BC=10,∠B=∠BCO=∠BAO=90°,
在RT△ABE中,∵AE=10,AB=8,
∴EB=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴EC=4,设DO=DE=x,
在RT△DCE中,∵CD2+CE2=DE2,
∴(8-a)2+42=a2,
∴a=5,
∴点D(0,5),点E(4,8),设直线DE为y=kx+b,
∴$\left\{\begin{array}{l}{b=5}\\{4k+b=8}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=5}\end{array}\right.$,
∴直线DE为:y=$\frac{3}{4}x$+5.
故选A.
点评 本题考查翻折变换、待定系数法确定一次函数的解析式,解题的关键是巧妙利用勾股定理,用方程的思想去思考问题,属于中考常考题型.

练习册系列答案
相关题目
2. 如图,已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
如图,已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
 如图,已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
如图,已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )| A. | 40° | B. | 80° | C. | 160° | D. | 120° |
 如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB=75°.
如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB=75°. (1)在平面直角坐标系中,描出下列4个点:A (-1,0),B (5,1),C (3,4);
(1)在平面直角坐标系中,描出下列4个点:A (-1,0),B (5,1),C (3,4); 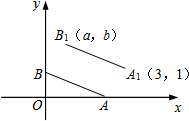 如图,A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,A1、B1的坐标分别为(3,1)、(a,b),则a+b的值为3.
如图,A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,A1、B1的坐标分别为(3,1)、(a,b),则a+b的值为3.