题目内容
3. (1)在平面直角坐标系中,描出下列4个点:A (-1,0),B (5,1),C (3,4);
(1)在平面直角坐标系中,描出下列4个点:A (-1,0),B (5,1),C (3,4); (2)顺次连接A,B,C,组成三角形ABC,求△ABC的面积.
分析 (1)找到各点的横坐标和纵坐标,分别向x轴和y轴作垂线,即可找到点A、B、C.
(2)△ABC的面积可转化为“梯形ACDE的面积-△ABE的面积-△BCD的面积”.
解答  解:(1)如图;
解:(1)如图;
(2)如图,
S△ABC=S梯形ACDE-S△ABE-S△BCD
=$\frac{1}{2}$×(2+6)×4-$\frac{1}{2}$×6×1-$\frac{1}{2}$×3×2
=16-3-3
=10.
点评 此题考查了坐标与图形的性质,将三角形补成梯形和三角形是解题的关键,此法被称为“割补法”.

练习册系列答案
相关题目
14.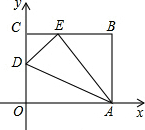 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )
 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )| A. | y=$\frac{3}{4}$x+5 | B. | y=$\frac{2}{5}$x+5 | C. | y=$\frac{1}{4}$x+5 | D. | y=$\frac{4}{5}$x+5 |
18.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
| A. | 12 | B. | 10 | C. | 7.5 | D. | 5 |
8.二次根式$\frac{1}{{\sqrt{x+1}}}$在实数范围有意义,则x的取值范围是( )
| A. | x≥-1 | B. | x≠-1 | C. | x>-1 | D. | x≤-1 |
 如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的三角形,请你帮助小华作出来.
如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的三角形,请你帮助小华作出来.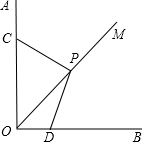 在平面直角坐标系中,O为坐标原点,∠AOB=90°,OM是∠AOB的平分线,PC⊥PD.PC=2,
在平面直角坐标系中,O为坐标原点,∠AOB=90°,OM是∠AOB的平分线,PC⊥PD.PC=2,