题目内容
5.对于同一平面内的三条直线a,b,c有下列五个论断:①a∥c;②b∥c;③a⊥b;④a∥b;⑤a⊥c,以其中两个论断为条件,一个论断为结论,请写出两个正确的不同类型的命题:如果①a∥c,②b∥c,那么④a∥b;如果③a⊥b,⑤a⊥c,那么②b∥c.分析 根据平行线的判定或性质写两个命题即可.
解答 解:如果①a∥c;②b∥c;那么④a∥b;
如果③a⊥b;⑤a⊥c,那么②b∥c.
故答案为如果①a∥c,②b∥c,那么④a∥b;如果③a⊥b,⑤a⊥c,那么②b∥c.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列说法中正确的是( )
| A. | 两个互补的角中必有一个是钝角 | |
| B. | 一个角的补角一定比这个角大 | |
| C. | 互补的两个角中至少有一个角大于或等于直角 | |
| D. | 相等的角一定互余 |
17.若两条平行线被第三条直线所截,则一对同旁内角的角平分线( )
| A. | 互相平行 | B. | 互相垂直 | C. | 相交但不垂直 | D. | 互相垂直或平行 |
4.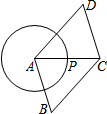 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
