题目内容
13.若质数p,q满足:3q-p-4=0,p+q<111,则pq的最大值为1007.分析 根据已知分别得出q,p的取值范围,进而结合质数的定义得出p,q的最值,进而得出答案.
解答 解:∵3q-p-4=0,
∴p=3q-4
∵p+q<111,
∴3q+q<111,
解得:q<28.75,
∵3q-p-4=0,
∴3q=p+4,
则q=$\frac{p+4}{3}$,
∵p+q<111,
∴$\frac{p+4}{3}$+q<111,
解得:p<82.25,
∵pq的最大,
∴当q取最大质数23时,p=65不合题意舍去,
则q=19时,P=53,此时符合题意,
故pq的最大值为:19×53=1007.
故答案为:1007.
点评 此题主要考查了质数的定义以及不等式的解法等知识,分别得出q,p的取值范围是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
 如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
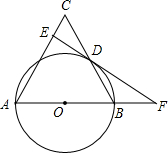 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,作DE⊥AC,垂足为点E,ED与AB的延长线交于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,作DE⊥AC,垂足为点E,ED与AB的延长线交于点F.
 已知CA=CB,CD=CE,B、C、E在同一条直线上,∠BCA=∠DCE=60°.
已知CA=CB,CD=CE,B、C、E在同一条直线上,∠BCA=∠DCE=60°.