题目内容
17.若两条平行线被第三条直线所截,则一对同旁内角的角平分线( )| A. | 互相平行 | B. | 互相垂直 | C. | 相交但不垂直 | D. | 互相垂直或平行 |
分析 作出图形,然后根据两直线平行,同旁内角互补以及角平分线的定义可得∠1+∠2=90°,再根据三角形的内角和定理求出∠C=90°,从而得解.
解答  解:如图,∵a∥b,
解:如图,∵a∥b,
∴∠DAB+∠ABE=180°,
∵AC、BC分别是角平分线,
∴∠1=$\frac{1}{2}$∠DAB,∠2=$\frac{1}{2}$∠ABE,
∴∠1+∠2=$\frac{1}{2}$×180°=90°,
∴∠C=180°-(∠1+∠2)=180°-90°=90°,
∴AC⊥BC,
∴同旁内角的平分线互相垂直.
故选:B.
点评 本题考查了平行线的性质,用到的知识点是两直线平行,同旁内角互补,角平分线的定义,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
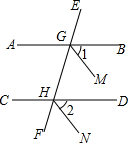 已知∠AGE=∠DHF,∠1=∠2,则图中的平行线有几对?分别是?为什么?
已知∠AGE=∠DHF,∠1=∠2,则图中的平行线有几对?分别是?为什么? 如图,菱形ABCD边长为2cm,∠ABC=60°,且M是BC边的中点,P是对角线BD上一动点,则PM+PC的最小值为$\sqrt{3}$.
如图,菱形ABCD边长为2cm,∠ABC=60°,且M是BC边的中点,P是对角线BD上一动点,则PM+PC的最小值为$\sqrt{3}$. 如图,已知AB∥CF,E为DF的中点,若AB=9cm,CF=5cm,求BD的长.
如图,已知AB∥CF,E为DF的中点,若AB=9cm,CF=5cm,求BD的长.