题目内容
4．先化简，再求值：（1-$\frac{1}{x+1}$）÷$\frac{x-2}{x+1}$，其中x满足x2=1．分析 首先化简（1-$\frac{1}{x+1}$）÷$\frac{x-2}{x+1}$，然后根据x满足x2=1，可得：x=±1，据此求出原式的值是多少即可．
解答 解：（1-$\frac{1}{x+1}$）÷$\frac{x-2}{x+1}$
=$\frac{x}{x+1}$÷$\frac{x-2}{x+1}$
=$\frac{x}{x-2}$
∵x满足x2=1，
∴x=±1，
当x=-1时，代数式无意义，
∴x=1，
当x=1时，
原式=$\frac{1}{1-2}$=-1．
点评 此题主要考查了分式的化简求值问题，要熟练掌握，化简求值，一般是先化简为最简分式或整式，再代入求值．化简时不能跨度太大，而缺少必要的步骤．
练习册系列答案
名校课堂系列答案
相关题目
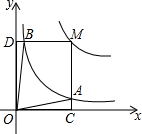反比例函数y=$\frac{a}{x}$（a＞0，a为常数）和y=$\frac{2}{x}$在第一象限内的图象如图所示，点M在y=$\frac{a}{x}$的图象上，MC⊥x轴于点C，交y=$\frac{2}{x}$的图象于点A；MD⊥y轴于点D，交y=$\frac{2}{x}$的图象于点B，当点M在y=$\frac{a}{x}$的图象上运动时，以下结论：①S△ODB=S△OCA；②四边形OAMB的面积不变；③当点A是MC的中点时，则点B是MD的中点．其中正确结论的序号是①②③．
如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA，AO，并延长AO交⊙O于点E，与PB的延长线交于点D．
16．某超市销售进价为2元的雪糕，在销售中发现，此商品的日销售单价x（元）与日销售量y（根）之间有如下关系：
（1）猜测并确定y和x之间的函数关系式；
（2）设此商品销售利润为W，求W与x的函数关系式，若物价局规定此商品最高限价为10元/根，你是否能求出商品日销售最大利润？若能请求出，不能请说明理由．
| 日销售单价x（元） | 3 | 4 | 5 | 6 |
| 日销售量y（根） | 40 | 30 | 24 | 20 |
（2）设此商品销售利润为W，求W与x的函数关系式，若物价局规定此商品最高限价为10元/根，你是否能求出商品日销售最大利润？若能请求出，不能请说明理由．