题目内容
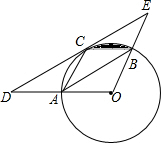
9. 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.(1)求证:PA是⊙O的切线;
(2)若cos∠CAO=$\frac{4}{5}$,且OC=6,求PB的长.
分析 (1)连接OB.先依据切线的性质证明∠PBO=90°,依据等腰三角形的性质可知∠OAB=∠OBA,由垂径定理可证明OP为AB的垂直平分线,则PA=PB,故此可证明∠PAB=∠PBA,然后依据等式的性质可得到∠PAO=∠PBO=90°;
(2)设AC=4k,AO=5k,由勾股定理可知OC=3k,在Rt△OAC中,利用锐角三角函数的定义先求得OA的长,在Rt△APO中利用锐角三角函数的定义可求得PA的长,最后依据切线长定理可求得PB的长.
解答 解:(1)连接OB.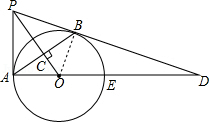
∵OA=OB,
∴∠OAB=∠OBA.
∵OP⊥AB,
∴AC=BC.
∴OP是AB的垂直平分线,
∴PA=PB.
∴∠PAB=∠PBA.
∴∠PAO=∠PBO.
∵PD为⊙O的切线,
∴∠OBP=90°.
∴∠PAO=90°.
∴PA是⊙O的切线.
(2)设AC=4k,AO=5k,由勾股定理可知OC=3k,
∴sin∠CAO=$\frac{3}{5}$,tan∠COA=$\frac{4}{3}$
∴$\frac{CO}{OA}$=$\frac{3}{5}$,即$\frac{6}{OA}$=$\frac{3}{5}$,解得OA=10.
∵tan∠POA=$\frac{AP}{AO}$=$\frac{4}{3}$,
∴$\frac{AP}{10}$=$\frac{4}{3}$,解得AP=$\frac{40}{3}$.
∵PA和PB均为⊙的切线,
∴PB=PA=$\frac{40}{3}$.
点评 本题主要考查的是切线的性质和判定、锐角三角函数的定义、勾股定理的应用,掌握切线的判定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知直角三角形的一直角边长为$\sqrt{5}$,斜边上的高为2,则这个直角的斜边长为( )
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{5\sqrt{2}}{2}$ |
14.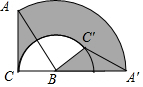 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
 如图,C是线段AB的中点.
如图,C是线段AB的中点.
 如图,?AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E.
如图,?AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E.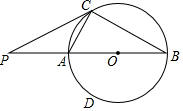 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.