题目内容
13.2016年底郑州市雾霾天气趋于严重,某商场根据民众健康需要,从厂家购进了A,B两种型号的空气净化器,如果销售15台A型和10台B型空气净化器的利润为6000元,销售10台A型和15台B型空气净化器的利润为6500元.(1)求每台A型空气净化器和B型空气净化器的销售利润;
(2)该商场计划一次购进两种型号的空气净化器共160台,其中B型空气净化器的进货量不超过A型空气净化器的2倍,设购进A型空气净化器x台,这160台空气净化器的销售总利润为y元.
①求y关于x的函数关系式;
②该公司购进A型、B型空气净化器各多少台时,才能使销售总利润最大?
分析 (1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;
(2)①根据题意可以得到y与x的函数关系式;
②根据题意可以求得x的取值范围,由①中的函数关系,从而可以得到该公司购进A型、B型空气净化器各多少台时,才能使销售总利润最大.
解答 解:(1)设每台A型空气净化器得销售利润为a元,每台B型空气净化器的销售利润为b元,
$\left\{\begin{array}{l}{15a+10b=6000}\\{10a+15b=6500}\end{array}\right.$,得$\left\{\begin{array}{l}{a=200}\\{b=300}\end{array}\right.$,
即每台A型空气净化器得销售利润为200元,每台B型空气净化器的销售利润为300元;
(2)①由题意可得,
y=200x+(160-x)×300=-100x+48000,
即y关于x的函数关系式是y=-100x+48000;
②由题意可得,
160-x≤2x,得x≥$53\frac{1}{3}$,
∵y=-100x+48000,
∴x=54时,y取得最大值,此时,160-x=106,
即该公司购进A型、B型空气净化器分别为54台、106台时,才能使销售总利润最大.
点评 本题考查一次函数的应用、解二元一次方程组,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
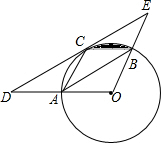 如图,?AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E.
如图,?AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E.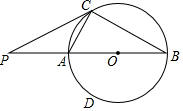 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.




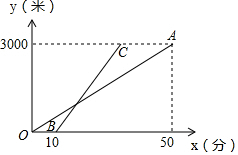 波波和爸爸两人以相同路线从家出发,步行前往公园.图中OA、BC分别表示爸爸和波波所走的路程y(米)与爸爸步行的时间x(分)的函数图象,已知爸爸从家步行到公园所花的时间比波波的2倍还多10分钟.则在步行过程中,他们父子俩相距的最远路程是1200米.
波波和爸爸两人以相同路线从家出发,步行前往公园.图中OA、BC分别表示爸爸和波波所走的路程y(米)与爸爸步行的时间x(分)的函数图象,已知爸爸从家步行到公园所花的时间比波波的2倍还多10分钟.则在步行过程中,他们父子俩相距的最远路程是1200米.