题目内容
3．（1）若两个相似三角形的面积比为1：2，则它们的相似比为$\sqrt{2}$：2；（2）若两个相似三角形的周长比为3：2，则这两个相似三角形的相似比为3：2；
（3）若两个相似三角形对应高的比为2：3，它们周长的差是25，那么较大三角形的周长是75．
分析 （1）根据相似三角形面积的比等于相似比的平方解答；
（2）根据相似三角形周长的比等于相似比解答；
（3）相似三角形对应高的比等于相似比和相似三角形周长的比等于相似比列出方程，解方程即可．
解答 解：（1）若两个相似三角形的面积比为1：2，则它们的相似比为$\sqrt{2}$：2；
（2）若两个相似三角形的周长比为3：2，则这两个相似三角形的相似比为3：2；
（3）∵两个相似三角形对应高的比为2：3，
∴它们周长的比是2：3，
设较小的三角形的周长为2x，则较大的三角形的周长为3x，
由题意得，3x-2x=25，
解得，x=25，
则3x=75，
∴较大三角形的周长是75．
故答案为：（1）$\sqrt{2}$：2；（2）3：2；（3）75．
点评 本题考查的是相似三角形的性质，相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比
练习册系列答案
相关题目
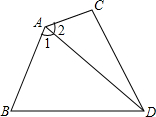如图，AB=2AC，∠1=∠2、DA=DB，求证：DC⊥AC．