题目内容
13.已知抛物线的顶点坐标为(-1,2),且过点(1,-2).(1)求该抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标.
分析 (1)设抛物线的解析式为y=a(x-h)2+k,再把顶点坐标为(-1,2)和点(1,-2)代入即可得出抛物线的解析式;
(2)令x=0,得出与y轴的交点坐标,再令y=0,得出与x轴的交点坐标.
解答 解:(1)设抛物线的解析式为y=a(x-h)2+k,
∵抛物线的顶点坐标为(-1,2)且过点(1,-2),
∴a(1+1)2+2=-2,
∴a=-1,
∴抛物线的解析式为y=-(x+1)2+2,
(2)令x=0,得y=1,与y轴的交点坐标(0,1),
令y=0,得x=$\sqrt{2}$-1或-$\sqrt{2}$-1,
∴与x轴的交点坐标为($\sqrt{2}$-1,0),(-$\sqrt{2}$-1,0).
点评 本题考查了用待定系数法求二次函数的解析式,同时还考查了抛物线与坐标轴的交点问题等知识,难度不大.

练习册系列答案
相关题目
17.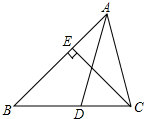 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
 如图,已知AB和CD是⊙0的两条弦,$\widehat{AC}=\widehat{BD}$,求证:AB=CD.
如图,已知AB和CD是⊙0的两条弦,$\widehat{AC}=\widehat{BD}$,求证:AB=CD.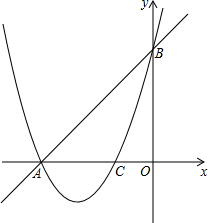 抛物线y=ax2+bx+3与y轴交于点B,与x轴负半轴交于点A、C(点A在C的左侧),C(-1,0),tan∠ABC=$\frac{1}{2}$,求抛物线的解析式.
抛物线y=ax2+bx+3与y轴交于点B,与x轴负半轴交于点A、C(点A在C的左侧),C(-1,0),tan∠ABC=$\frac{1}{2}$,求抛物线的解析式.