题目内容
14. 如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
分析 欲证明CE=DF,只要证明△CEB≌△DFC即可.
解答 证明:∵ABCD是正方形,
∴AB=BC=CD,∠EBC=∠FCD=90°,
又∵E、F分别是AB、BC的中点,
∴BE=CF,
在△CEB和△DFC中,
$\left\{\begin{array}{l}{BC=CD}\\{∠B=∠DCF}\\{BE=CF}\end{array}\right.$,
∴△CEB≌△DFC,
∴CE=DF.
点评 本题考查正方形的性质、全等三角形的判定和性质,解题的关键是熟练掌握正方形的性质以及全等三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
5. 如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
 如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖,如图:
那么被遮盖的两个数据依次是( )
| 编号 | 1 | 2 | 3 | 4 | 5 | 方差 | 平均成绩 |
| 得分 | 38 | 34 | ■ | 37 | 40 | ■ | 37 |
| A. | 35,2 | B. | 36,4 | C. | 35,3 | D. | 36,3 |
6.sin30°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
3.下列四个数中,最大的数是( )
| A. | -2 | B. | $\frac{1}{3}$ | C. | 0 | D. | 6 |
 如图,⊙O1和⊙O2是外切于点P的两个等圆,点A、B分别在⊙O1、⊙O2上,∠APB=90°,和⊙O1、⊙O2的另一个交点分别是C、D.求证:CD=O1O2.
如图,⊙O1和⊙O2是外切于点P的两个等圆,点A、B分别在⊙O1、⊙O2上,∠APB=90°,和⊙O1、⊙O2的另一个交点分别是C、D.求证:CD=O1O2. 解不等式$\frac{1+x}{3}<x-1$,并将解集在数轴上表示出来.
解不等式$\frac{1+x}{3}<x-1$,并将解集在数轴上表示出来. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.
如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.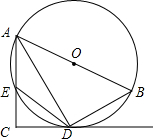 如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD于点C,交⊙O于点E,连接AD、BD、ED.
如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD于点C,交⊙O于点E,连接AD、BD、ED.