题目内容
12.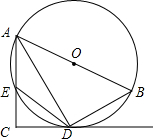 如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD于点C,交⊙O于点E,连接AD、BD、ED.
如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD于点C,交⊙O于点E,连接AD、BD、ED.(1)求证:BD=ED;
(2)若CE=3,CD=4,求AB的长.
分析 (1)连接OD、OE,由切线的性质可知OD⊥CD,从而可证明AC∥OD,接下来由平行线的性质、等腰三角形的性质可证明∠EOD=∠DOB;
(2)在△CED中依据勾股定理可求得ED的长,从而得到BD的长,接下来证明△ECD∽△BDA,依据相似三角形的性质可求得AB的长.
解答 解:(1)证明:连接OD、OE.
∵CD切⊙O于点D,
∴OD⊥CD.
∵AC⊥CD,
∴OD∥AC.
∴∠EAO=∠DOB,∠AEO=∠EOD.
又∵∠EAO=∠AEO,
∴∠EOD=∠DOB.
∴BD=ED.
(2)∵AC⊥CD,
∴∠ACD=90°
又∵CE=3,CD=4,
∴ED=5.
∵BD=ED,
∴BD=5.
∵AB为⊙O的直径,
∴∠ADB=90°
∴∠ACD=∠ADB.
∵四边形ABDE内接于⊙O,
∠CED=∠B,
∴△CDE∽△DAB.
∴$\frac{CE}{DB}=\frac{DE}{AB}$.
∴$\frac{3}{5}=\frac{5}{AB}$.
∴AB=$\frac{25}{3}$.
点评 本题主要考查的是切线的性质、相似三角形的性质和判定、平行线的性质,证得OD∥AC、△CDE∽△DAB是解题的关键.

练习册系列答案
相关题目
20.如图,三个图形是由立体图形展开得到的,相应的立体图形顺序是( )


| A. | 圆柱、三棱柱、圆锥 | B. | 圆锥、三棱柱、圆柱 | ||
| C. | 圆柱、三棱锥、圆锥 | D. | 圆柱、三棱柱、半球 |
 如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.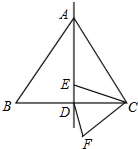 如图,在△ABC中,AB=AC=2$\sqrt{2}$,∠BAC=90°,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转45°得到FC,连接DF,则在点E运动过程中,DF的最小值是2-$\sqrt{2}$.
如图,在△ABC中,AB=AC=2$\sqrt{2}$,∠BAC=90°,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转45°得到FC,连接DF,则在点E运动过程中,DF的最小值是2-$\sqrt{2}$.
 北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市机动车的保有量约562万辆,你的预估理由是从各年的保有量增长看,汽车已趋于饱和,故2016年保有量相对2015年变化不大.
北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市机动车的保有量约562万辆,你的预估理由是从各年的保有量增长看,汽车已趋于饱和,故2016年保有量相对2015年变化不大.