题目内容
9. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.
如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.
分析 当直线l在直线CE上方时,连接DE交直线l于M,只要证明△DFM是等腰直角三角形即可利用DF=$\sqrt{2}$DM解决问题,当直线l在直线EC下方时,由∠DEF1=∠BEF1=∠DF1E,
得到DF1=DE,由此即可解决问题.
解答 解:如图,当直线l在直线CE上方时,连接DE交直线l于M,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,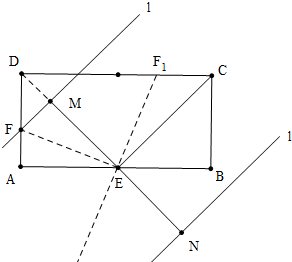
∵AB=4,AD=BC=2,
∴AD=AE=EB=BC=2,
∴△ADE、△ECB是等腰直角三角形,
∴∠AED=∠BEC=45°,
∴∠DEC=90°,
∵l∥EC,
∴ED⊥l,
∴EM=2=AE,
∴点A、点M关于直线EF对称,
∵∠MDF=∠MFD=45°,
∴DM=MF=DE-EM=2$\sqrt{2}$-2,
∴DF=$\sqrt{2}$DM=4-2$\sqrt{2}$.
当直线l在直线EC下方时,
∵∠DEF1=∠BEF1=∠DF1E,
∴DF1=DE=2$\sqrt{2}$,
综上所述DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.
故答案为2$\sqrt{2}$或4-2$\sqrt{2}$.
点评 本题考查翻折变换、矩形的性质、等腰直角三角形的性质和判定,解题的关键是正确画出图形,注意有两种情形,属于中考常考题型.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 △ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.
△ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.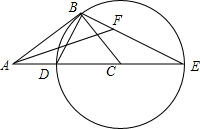 如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.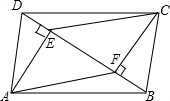 四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.
四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F. 如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.