题目内容
5. 如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据正五边形的性质得到∠ABE=∠AEB=∠EAD=36°,根据三角形的内角和即可得到结论;由于∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,得到∠AEN=∠ANE,根据等腰三角形的判定定理得到AE=AN,同理DE=DM,根据相似三角形的性质得到$\frac{AE}{AD}=\frac{AM}{AE}$,等量代换得到AN2=AM•AD;根据AE2=AM•AD,列方程得到MN=3-$\sqrt{5}$;在正五边形ABCDE中,由于BE=CE=AD=1+$\sqrt{5}$,得到BH=$\frac{1}{2}$BC=1,根据勾股定理得到EH=$\sqrt{(1+\sqrt{5})^{2}-{1}^{2}}$=$\sqrt{5+2\sqrt{5}}$,根据三角形的面积得到结论.
解答 解:∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°-∠EAM-∠AEM=108°,故①正确;
∵∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,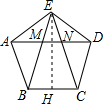
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE,
∴$\frac{AE}{AD}=\frac{AM}{AE}$,
∴AE2=AM•AD;
∴AN2=AM•AD;故②正确;
∵AE2=AM•AD,
∴22=(2-MN)(4-MN),
∴MN=3-$\sqrt{5}$;故③正确;
在正五边形ABCDE中,
∵BE=CE=AD=1+$\sqrt{5}$,
∴BH=$\frac{1}{2}$BC=1,
∴EH=$\sqrt{(1+\sqrt{5})^{2}-{1}^{2}}$=$\sqrt{5+2\sqrt{5}}$,
∴S△EBC=$\frac{1}{2}$BC•EH=$\frac{1}{2}$×2×$\sqrt{5+2\sqrt{5}}$=$\sqrt{5+2\sqrt{5}}$,故④错误;
故选C.
点评 本题考查了相似三角形的判定和性质,勾股定理,正五边形的性质,熟练掌握正五边形的性质是解题的关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | 必然事件的概率是1 | |
| B. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖 | |
| C. | 了解一批灯泡的使用寿命适合用抽样调查 | |
| D. | 数据1、2、2、3的平均数是2 |
 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |




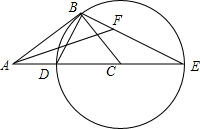 如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.

 如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.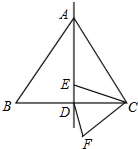 如图,在△ABC中,AB=AC=2$\sqrt{2}$,∠BAC=90°,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转45°得到FC,连接DF,则在点E运动过程中,DF的最小值是2-$\sqrt{2}$.
如图,在△ABC中,AB=AC=2$\sqrt{2}$,∠BAC=90°,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转45°得到FC,连接DF,则在点E运动过程中,DF的最小值是2-$\sqrt{2}$.