题目内容
4. 如图,⊙O1和⊙O2是外切于点P的两个等圆,点A、B分别在⊙O1、⊙O2上,∠APB=90°,和⊙O1、⊙O2的另一个交点分别是C、D.求证:CD=O1O2.
如图,⊙O1和⊙O2是外切于点P的两个等圆,点A、B分别在⊙O1、⊙O2上,∠APB=90°,和⊙O1、⊙O2的另一个交点分别是C、D.求证:CD=O1O2.
分析 连接O1O2,AO1,BO2,作O1M⊥AD于M,O2N⊥AD于N,先证明四边形ABO2O1是平行四边形,再证明AC=BD即可解决问题.
解答 证明:连接O1O2,AO1,BO2,作O1M⊥AD于M,O2N⊥AD于N.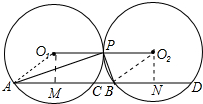 ∵⊙O1和⊙O2外切于点P,
∵⊙O1和⊙O2外切于点P,
∴接O1O2经过点P,
∵PA⊥PB,
∴∠APB=90°,
∴∠PAB+∠PBA=90°,∠APO1+∠BPO2=90°,
∵O1A=O1P,O2P=O2B,
∴∠O1AP=∠O1PA,∠O2PB=∠O2BP,
∴∠O1AB+∠O2BA=∠O1AP+∠PAB+∠PBA+∠O2BP=180°,
∴AO1∥BO2,∵AO1=BO2,
∴四边形ABO2O1是平行四边形,
∴AB=O1O2=2r.O1O2∥AB,
∵O1M∥O2N,
∴四边形MNO2O1是平行四边形,
∴O1M=O2N,∵O1M⊥AD,O2N⊥AD,
∴AC=BD(弦心距相等弦相等),
∴AB=CD,
∴CD=2r.
点评 本题考查了相切两个圆的性质,平行四边形的判定和性质等知识,解题的关键是添加辅助线,构造特殊四边形,学会条件常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
14.计算:
(1)(-x2y5)•(xy)3
(2)4a(a-b+1)
(3)10032(简便计算)
(4)x2-(x+1)(x-1)
(5)先化简再求值:(a-2)2+2(a-1)(a+2),其中a=-2.
(1)(-x2y5)•(xy)3
(2)4a(a-b+1)
(3)10032(简便计算)
(4)x2-(x+1)(x-1)
(5)先化简再求值:(a-2)2+2(a-1)(a+2),其中a=-2.
15.下列说法错误的是( )
| A. | 必然事件的概率是1 | |
| B. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖 | |
| C. | 了解一批灯泡的使用寿命适合用抽样调查 | |
| D. | 数据1、2、2、3的平均数是2 |
12.在下列四组线段中,能组成直角三角形的是( )
| A. | a=9 b=12 c=15 | B. | a=32 b=42 c=52 | C. | a=12 b=18 c=22 | D. | a:b:c=1:1:2 |
9.下列说法错误的是( )
| A. | 必然事件的概率为1 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的方差为8.5 | |
| D. | 若某抽奖活动的中奖率为40%,则参加这种活动10次必有4次中奖 |
16. 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
 △ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.
△ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.



 如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.