题目内容
5.同时投掷两颗骰子,若P(a)表示两颗骰子面朝上的点数之和为a的概率,则P(1)+P(2)+P(3)+P(4)+P(5)=$\frac{5}{18}$.分析 首先根据题列出表格,然后由表格即可求得所有等可能的结果与面朝上的点数之和分别为1,2,3,4,5的情况,再利用概率公式即可求得答案.
解答 解:列表得:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
∴P (1)=0,P (2)=$\frac{1}{36}$,P (3)=$\frac{2}{36}$,P (4)=$\frac{3}{36}$,P (5)=$\frac{4}{36}$,
∴P (1)+P (2)+P (3)+P (4)+P (5)=$\frac{10}{36}=\frac{5}{18}$.
故答案为:$\frac{5}{18}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
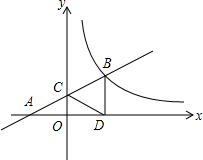 如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.
如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.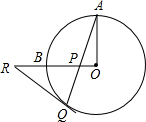 如图,OA、OB是⊙O的两条互相垂直的半径,P为OB上任一点,AP的延长线交⊙O于点Q,过点Q作⊙O的切线交OB的延长线于点R,求证:RP=RQ.
如图,OA、OB是⊙O的两条互相垂直的半径,P为OB上任一点,AP的延长线交⊙O于点Q,过点Q作⊙O的切线交OB的延长线于点R,求证:RP=RQ.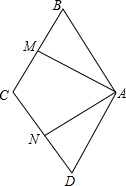 已知:如图,在菱形ABCD中,∠BAD=120°,点M,N分别在BC和CD上,且∠MAN=60°.
已知:如图,在菱形ABCD中,∠BAD=120°,点M,N分别在BC和CD上,且∠MAN=60°.