题目内容
17.某医院为了提高服务质量,进行了下面的调查:当还未开始挂号时,有N个人已经在排队挂号,开始挂号后排队的人数平均每分钟增加M人.假定挂号的速度是每窗口每分钟K个人,当开放一个窗口时,40分钟后恰好不会出现排队现象;若同时开放两个窗口时,则15分钟后恰好不会出现排队现象.根据以上信息,若要求8分钟后不出现排队现象,则需要同时开放的窗口至少应有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
分析 由已知中当还未开始挂号时,有N个人已经在排队等候挂号.开始挂号后排队的人数平均每分钟增加M人.挂号的速度是每窗口每分钟K个人,当开放一个窗口时,40分钟后恰好不会出现排队现象;若同时开放两个窗口时,则15分钟后恰好不会出现排队现象.我们可以构造关于M,N的方程组,求出M,N,K的关系,进而由8分钟后不出现排队现象,构造一个关于n的不等式,解不等式即可得到答案.
解答 解:设要同时开放n个窗口才能满足要求,
则$\left\{\begin{array}{l}{N+40M=40K}\\{N+15M=15K×2}\end{array}\right.$,
解得:$M=\frac{2}{5}K,N=24K$,
∴N+8M≤8Kn
∴24K+3.2K≤8Kn
解得n≥3.4.
故至少同时开放4个窗口才能满足要求.
故选A.
点评 本题以函数为载体,考查函数模型的选择与应用,在利用函数模型,解答应用题时,解答的关键是根据已知条件求出函数的解析式.

练习册系列答案
相关题目
8.若4x2-5xy-6y2=0,其中xy≠0,则$\frac{x+y}{x-y}$的值为( )
| A. | -3或$\frac{1}{7}$ | B. | 3或-$\frac{1}{7}$ | C. | 3 | D. | $\frac{1}{7}$ |
12.下列说法正确的是( )
| A. | “明天会下雨”是必然事件 | |
| B. | 想了解“五•一”期间福州市各家庭的消费情况,适合的调查方式是抽样调查 | |
| C. | 正方形是轴对称图形,不是中心对称图形 | |
| D. | 120000用科学记数法表示是1.2×106 |
6.一件商品的原价是100元,经过两次提价后的价格为123元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
| A. | 100(1+x)=123 | B. | 100(1-x)=123 | C. | 100(1+x)2=123 | D. | 100(1-x)2=123 |
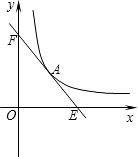 如图,已知:A(m,4)是一次函数y=kx+b与反比例函数y=$\frac{12}{x}$的公共点
如图,已知:A(m,4)是一次函数y=kx+b与反比例函数y=$\frac{12}{x}$的公共点