题目内容
4.已知在直线l有三个点A、B、C,线段AB=6cm,BC=4cm,若M、N分别是AB、BC的中点(1)求中点M、N间的距离.(画图,并写出简单过程)
(2)分析(1)的解答过程,若AB=acm,BC=bcm,且a>b,其他条件不变,此时M、N间的距离是多少?(直接写出答案)MN=$\frac{a-b}{2}$或$\frac{a+b}{2}$.
分析 分类讨论点C在AB上,点C在AB的延长线上,根据线段的中点的性质,可得BM、BN的长,根据线段的和差,可得答案.
解答 解:(1)①点C在线段AB上,如图:
∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{2}$CB=2,
∴MN=BM-BN=3-2=1cm;
②点C在线段AB的延长线上,如图:

∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{2}$CB=2,
∴MN=MB+BN=3+2=5cm.
(2)①点C在线段AB上,如图:
∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=$\frac{1}{2}$a,BN=$\frac{1}{2}$CB=$\frac{1}{2}$b,
∴MN=BM-BN=$\frac{a-b}{2}$cm;
(2)点C在线段AB的延长线上,如图:

∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=$\frac{1}{2}$a,BN=$\frac{1}{2}$CB=$\frac{1}{2}$b,
∴MN=MB+BN=$\frac{a+b}{2}$cm.
故答案为:$\frac{a-b}{2}$或$\frac{a+b}{2}$.
点评 本题考查了两点间的距离,分类讨论是解题关键,根据线段中点的性质,线段的和差,可得出答案.

练习册系列答案
相关题目
15.2012伦敦奥运会火炬决定不设海外路线,其国内传递路程约为1.28万公里,近似数1.28万是精确到( )
| A. | 十分位 | B. | 百分位 | C. | 千位 | D. | 百位 |
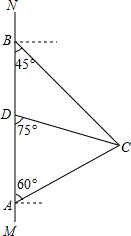 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.