题目内容
2.阅读下面的材料,并完成后面提出的问题.(1)如图1中,AC∥DB,请你探究一下∠M,∠A与∠B的数量有何关系,并说明理由
(2)如图2中,当点M向左移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?
(3)如图3中,当点M向上移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?
(4)如图4中,当点M向下移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?
写出对应图形的数量关系,并选其中的一个图形加以证明

分析 (1)先过点M作ME∥AC,得出AC∥ME∥DB,进而得到∠A=∠AME,∠B=∠BME,再根据角的和差关系即可得出∠A+∠B=∠AME+∠BME=∠AMB;
(2)先过点M作MF∥AC,得出AC∥MF∥DB,进而得到∠A+∠AMF=180°,∠B+∠BMF=180°,再根据角的和差关系即可得出∠AMB+∠A+∠B=∠A+∠AMF+∠B+∠BMF=360°;
(3)先过点M作MG∥AC,得出AC∥MG∥DB,进而得到∠A=∠AMG,∠B=∠BMG,再根据角的和差关系即可得出∠A-∠B=∠AMG-∠BMG=∠AMB;
(4)先过点M作MH∥AC,得出AC∥MH∥DB,进而得到∠A=∠AMH,∠B=∠BMH,再根据角的和差关系即可得出∠B-∠A=∠BMH-∠AMH=∠AMB.
解答 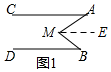 解:(1)∠AMB=∠A+∠B.
解:(1)∠AMB=∠A+∠B.
理由:如图1,过点M作ME∥AC,
∵AC∥DB,
∴AC∥ME∥DB,
∴∠A=∠AME,∠B=∠BME,
∴∠A+∠B=∠AME+∠BME=∠AMB;
(2)∠AMB+∠A+∠B=360°.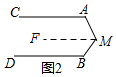
理由:如图2,过点M作MF∥AC,
∵AC∥DB,
∴AC∥MF∥DB,
∴∠A+∠AMF=180°,∠B+∠BMF=180°,
∴∠AMB+∠A+∠B=∠A+∠AMF+∠B+∠BMF=360°;
(3)∠A-∠B=∠AMB.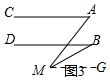
理由:如图3,过点M作MG∥AC,
∵AC∥DB,
∴AC∥MG∥DB,
∴∠A=∠AMG,∠B=∠BMG,
∴∠A-∠B=∠AMG-∠BMG=∠AMB;
(4)∠B-∠A=∠AMB.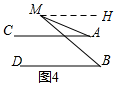
理由:如图4,过点M作MH∥AC,
∵AC∥DB,
∴AC∥MH∥DB,
∴∠A=∠AMH,∠B=∠BMH,
∴∠B-∠A=∠BMH-∠AMH=∠AMB.
点评 本题主要考查了平行线的性质,解决问题的关键是作辅助线,根据两直线平行,同旁内角互补;两直线平行,内错角相等进行求解.

 名校课堂系列答案
名校课堂系列答案| A. | x=2 | B. | x=0 | C. | x1=2,x2=0 | D. | x1=-2,x2=0 |




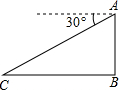 如图,飞机A在目标B的正上方1 000米处,飞行员测得地面目标C的俯角为30°,则地面目标B、C之间的距离是1000$\sqrt{3}$.
如图,飞机A在目标B的正上方1 000米处,飞行员测得地面目标C的俯角为30°,则地面目标B、C之间的距离是1000$\sqrt{3}$.