题目内容
14．在同一平面直角坐标系中，函数y=kx+k与y=$\frac{k}{x}$（k≠0）的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 分两种情况讨论，当k＞0时，分析出一次函数和反比例函数所过象限；再分析出k＜0时，一次函数和反比例函数所过象限，符合题意者即为正确答案．
解答 解：①当k＞0时，y=kx+k过一、二、三象限；y=$\frac{k}{x}$过一、三象限；
②当k＜0时，y=kx+k过二、三、四象象限；y=$\frac{k}{x}$过二、四象限．
观察图形可知，只有A选项符合题意．
故选：A．
点评 本题主要考查了反比例函数的图象和一次函数的图象，熟悉两函数中k和b的符号对函数图象的影响是解题的关键．
练习册系列答案
相关题目
4．小明做了以下4道计算题：①（-1）2010=2010；②0-（-1）=-l；③-$\frac{1}{2}$+$\frac{1}{3}$=-$\frac{1}{6}$；④$\frac{1}{2}$÷（-$\frac{1}{2}$）=-1．其中做对的共有（ ）
| A． | 1道 | B． | 2道 | C． | 3道 | D． | 4道 |
9．要使二次根式$\sqrt{x-2}$有意义，x必须满足（ ）
| A． | x≤2 | B． | x≥2 | C． | x＜2 | D． | x＞2 |
19．-$\frac{1}{5}$的相反数是（ ）
| A． | -5 | B． | $\frac{1}{5}$ | C． | -$\frac{1}{5}$ | D． | 5 |
在四边形ABCD中，∠C=90，AB=AD，AB∥CD，AE平分∠BAD交BC于E，请你只用无刻度的直尺画出矩形BCDF（保留作图痕迹）
3．JDF学校2015年春季学期组织一次校园文化知识竞赛，准备期间，拟从A，B，C，D四套卷中抽取两套题进行模拟训练，A卷恰好被抽中的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | 以上都不对 |
4．
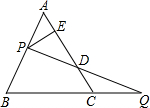如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（ ）
如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |