题目内容
12.方程x2-2|x|+k=0有2个不相等的根,求k的范围.分析 分x≥0和x<0两种情况考虑,利用配方法解一元二次方程可求出x的值,再根据方程x2-2|x|+k=0有2个不相等的根,即可得出关于k的一元一次不等式组,解之即可得出结论.
解答 解:当x≥0时,原方程为x2-2x+k=(x-1)2+k-1=0,
解得:x1=1-$\sqrt{1-k}$,x2=1+$\sqrt{1-k}$(1-k≥0);
当x<0时,原方程为x2+2x+k=(x+1)2+k-1=0,
解得:x3=-1-$\sqrt{1-k}$,x4=-1+$\sqrt{1-k}$(1-k≥0).
∵方程x2-2|x|+k=0有2个不相等的根,
∴$\left\{\begin{array}{l}{1-k≥0}\\{1-\sqrt{1-k}<0}\\{-1+\sqrt{1-k}≥0}\end{array}\right.$,
解得:k<0.
∴若方程x2-2|x|+k=0有2个不相等的根,k的取值范围为k<0.
点评 本题考查了配方法解一元二次方程以及解一元一次不等式组,利用配方法求出方程的根结合方程有两个不等的根找出关于k的一元一次不等式组是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
3.JDF学校2015年春季学期组织一次校园文化知识竞赛,准备期间,拟从A,B,C,D四套卷中抽取两套题进行模拟训练,A卷恰好被抽中的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 以上都不对 |
20. 如图为我县一月份某一天的天气预报,该天最高气温比最低气温高( )
如图为我县一月份某一天的天气预报,该天最高气温比最低气温高( )
 如图为我县一月份某一天的天气预报,该天最高气温比最低气温高( )
如图为我县一月份某一天的天气预报,该天最高气温比最低气温高( )| A. | -3℃ | B. | 7℃ | C. | 3℃ | D. | -7℃ |
17.下列各组代数式中,是同类项的为( )
| A. | abc2与3bac2 | B. | 2an2与-a2n | C. | 5与-2x | D. | -$\frac{1}{3}$a2y与$\frac{2}{3}$a2 |
4.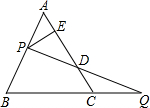 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
1.已知点A(-1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应,若点A′的坐标为(1,-3),则点B′的坐标为( )
| A. | (3,0) | B. | (3,-3) | C. | (3,-1) | D. | (-1,3) |
2.福布斯2016年全球富豪榜出炉,中国上榜人数仅次于美国,其中王健林以287亿美元的财富雄踞中国内地富豪榜榜首,这一数据用科学记数法可表示为( )
| A. | 0.287×1010美元 | B. | 0.287×1011美元 | C. | 2.87×1010美元 | D. | 2.87×1011美元 |

