题目内容
10.如图是一个按某种规律排列的数阵:
根据数阵的规律,第n行第一个数是$\sqrt{{n}^{2}-n+1}$.(用含n的代数式表示).
分析 观察不难发现,被开方数是从1开始的连续自然数,每一行的数据的个数是从2开始的连续偶数,求出n-1行的数据的个数,再加上1得到所求数的被开方数,然后写出算术平方根即可.
解答 解:前(n-1)行的数据的个数为2+4+6+…+2(n-1)=n(n-1),
所以,第n(n是整数,且n≥3)行第1个数是n(n-1)+1=n2-n+1,
所以,第n(n是整数,且n≥3)行第1个数是$\sqrt{{n}^{2}-n+1}$.
故答案为:$\sqrt{{n}^{2}-n+1}$.
点评 本题考查了算术平方根,观察数据排列规律,确定出前(n-1)行的数据的个数是解题的关键.

练习册系列答案
相关题目
20.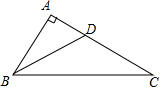 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )
 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )| A. | 5cm | B. | 12cm | C. | 13cm | D. | 不能确定 |
18.为了创建“全国文明城市”,我校志愿者小组成员从学校出发,在学校门口东西方向的道路上进行义务保洁.规定向东行为正,向西行为负,已知某志愿者一个下午的七次行走记录如表所示(单位:千米):
(1)该志愿者保洁结束时是否回到出发地点?如果没有,那么距离出发点多少千米?
(2)在第六次保洁时离出发地点最远;
(3)若每千米平均用时15分钟,则该志愿者完成这次保洁任务一共用时多少小时?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| +1 | -1.1 | +2 | +0.7 | -1 | +1.2 | -3 |
(2)在第六次保洁时离出发地点最远;
(3)若每千米平均用时15分钟,则该志愿者完成这次保洁任务一共用时多少小时?
5.下列算式能用平方差公式计算的是( )
| A. | (2m+n)(2n-m) | B. | (-m-n)(-m+n) | C. | (3m-n)(-3m+n) | D. | (-m-n)(m+n) |
 如图△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=15°,则∠DGB=65°.
如图△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=15°,则∠DGB=65°.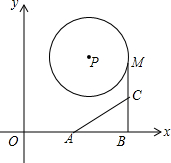 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是$\frac{3}{2}$.
如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是$\frac{3}{2}$.