题目内容
2.已知⊙O的半径OA=1,弦AB=1,求弦AB所对的圆周角的度数.分析 根据弦长等于半径,得这条弦和两条半径组成了等边三角形,则弦所对的圆心角是60°,要计算它所对的圆周角,应考虑两种情况:当圆周角的顶点在优弧上时,则根据圆周角定理,得此圆周角是30°;当圆周角的顶点在劣弧上时,则根据圆内接四边形的对角互补,得此圆周角是150°.
解答 解:根据题意,∵弦AB与两半径组成等边三角形,
∴AB所对的圆心角=60°,
①圆周角在优弧上时,圆周角=30°,
②圆周角在劣弧上时,圆周角=180°-30°=150°.
综上所述,弦AB所对圆周角的度数为30°或150°.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
13.在-1$\frac{1}{2}$,1.2,-2,0,-(-2),(-1)3中,负数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.实验:袋中装有8个黑球,4个白球,这些球的形状、大小、质地等完全相同,在看不到的条件下,随机地从袋子中摸出1个球.
我们把“摸到黑球”记为事件A,吧“摸到白球”记为事件B,填写下表并回答问题.
(1)事件A和事件B是随机事件吗?
(2)哪个事件发生的可能性大?
(3)你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论?
(4)为了尽可能获得正确结论,我们应该怎样做?
我们把“摸到黑球”记为事件A,吧“摸到白球”记为事件B,填写下表并回答问题.
| 事件A发生的次数 | 事件B发生的次数 | 结果(指哪个事件发生的次数多) | |
| 10次摸球 | |||
| 20次摸球 |
(2)哪个事件发生的可能性大?
(3)你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论?
(4)为了尽可能获得正确结论,我们应该怎样做?

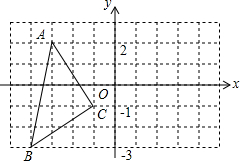 如图,在平面直角坐标系xOy中,
如图,在平面直角坐标系xOy中,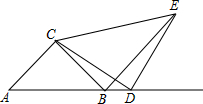 如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.
如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.