题目内容
15．
如图△ABC≌△ADE，BC的延长线交DA于F，交DE于G，∠D=25°，∠E=105°，∠DAC=15°，则∠DGB=65°．
分析 根据全等三角形对应角相等可得∠ACB=∠E，再求出∠ACF，然后根据三角形的内角和定理列式计算即可得解．
解答 解：∵△ABC≌△ADE，
∴∠ACB=∠E=105°，
∴∠ACF=180°-105°=75°，
在△ACF和△DGF中，∠D+∠DGB=∠DAC+∠ACF，
即25°+∠DGB=15°+75°，
解得∠DGB=65°．
故答案为：65°
点评 本题考查了全等三角形的性质，三角形的内角和定理，熟记性质并准确识图是解题的关键．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5．下列计算中，正确的是（ ）
| A． | 7ab-3ab=4 | B． | -$\frac{1}{3}$（6a-1）=-2a+1 | C． | x2y-2x2y=-x2y | D． | （-$\frac{1}{2}$）÷$\frac{1}{4}$×2=-1 |
6．意大利著名数学家斐波那契发现有这样一组数：1，1，2，3，5，8，13，…．其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的边长值分别构造正方形，再从左到右分别取前2个、前3个、前4个、前5个正方形拼成如图所示的若干个长方形并按序依次记为①、②、③、④、…．
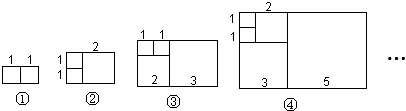
每个长方形的周长如表所示：
（1）仔细观察图形，表中的x=16，y=26．
（2）若按此规律继续拼长方形，则序号为⑩的长方形周长是466．
每个长方形的周长如表所示：
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
（2）若按此规律继续拼长方形，则序号为⑩的长方形周长是466．
3．计算6a3÷（-2a）的结果是（ ）
| A． | -3a2 | B． | -3a3 | C． | 3a2 | D． | 3a |
7．实验：袋中装有8个黑球，4个白球，这些球的形状、大小、质地等完全相同，在看不到的条件下，随机地从袋子中摸出1个球．
我们把“摸到黑球”记为事件A，吧“摸到白球”记为事件B，填写下表并回答问题．
（1）事件A和事件B是随机事件吗？
（2）哪个事件发生的可能性大？
（3）你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论？
（4）为了尽可能获得正确结论，我们应该怎样做？
我们把“摸到黑球”记为事件A，吧“摸到白球”记为事件B，填写下表并回答问题．
| 事件A发生的次数 | 事件B发生的次数 | 结果（指哪个事件发生的次数多） | |
| 10次摸球 | |||
| 20次摸球 |
（2）哪个事件发生的可能性大？
（3）你认为“10次摸球”和“20次摸球”哪种实验更能获得较正确的结论？
（4）为了尽可能获得正确结论，我们应该怎样做？
4．下列函数关系式中属于反比例函数的是（ ）
| A． | y=3x | B． | y=-$\frac{2}{x}$ | C． | y=x2+3 | D． | x+y=5 |