题目内容
6.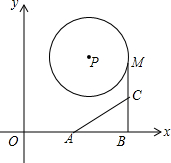 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是$\frac{3}{2}$.
如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是$\frac{3}{2}$.
分析 如图,连接OP交⊙P于M′,连接OM.因为OA=AB,CM=CB,所以AC=$\frac{1}{2}$OM,所以当OM最小时,AC最小,M运动到M′时,OM最小,由此即可解决问题.
解答 解:如图,连接OP交⊙P于M′,连接OM.
∵OA=AB,CM=CB,
∴AC=$\frac{1}{2}$OM,
∴当OM最小时,AC最小,
∴当M运动到M′时,OM最小,
此时AC的最小值=$\frac{1}{2}$OM′=$\frac{1}{2}$(OP-PM′)=$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查点与圆的位置关系、坐标与图形的性质、三角形中位线定理、最小值问题等知识,解题的关键是理解圆外一点到圆的最小距离以及最大距离,学会用转化的思想思考问题,所以中考常考题型.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

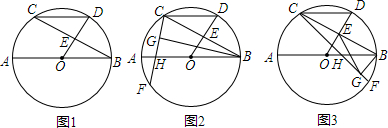
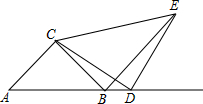 如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.
如图,已知△ABC,CA=CB,DC=DE,∠BCA=∠CDE=90°,D是AB延长线上一点.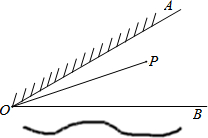 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.