题目内容
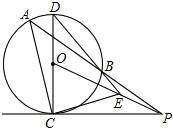 如图,PAB为⊙O的割线,PC切⊙O于C,CD为⊙O的直径,DB交PO于E.求证:AC⊥CE.
如图,PAB为⊙O的割线,PC切⊙O于C,CD为⊙O的直径,DB交PO于E.求证:AC⊥CE.考点:切线的性质
专题:证明题
分析:取AB的中点,利用垂径定理和切线的性质可证得P、F、O、C四点共圆,可证得△DOE∽△ACE,再结合条件可证明△DCE∽△ABC,结合圆周角定理可证得∠DBC=90°,可证得结论.
解答: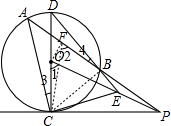 证明:取AB的中点F,连接OF、CF、BC,
证明:取AB的中点F,连接OF、CF、BC,
由垂径定理可知OF⊥AB,
∵PC是⊙O的切线,
∴∠OFP=90°=∠PCO,
∴P、F、O、C四点共圆,
∴∠1=∠2,
∴∠DOE=∠AFC,且∠D=∠A,
∴△DOE∽△AFC,
∴
=
=
=
,
又∵∠A=∠D,
∴△DCE∽△ABC,
∴∠DCE=∠ABC,
∴∠ACE=∠3+∠DCE=∠4+∠ABC=∠DBC=90°,
∴AC⊥CE.
 证明:取AB的中点F,连接OF、CF、BC,
证明:取AB的中点F,连接OF、CF、BC,由垂径定理可知OF⊥AB,
∵PC是⊙O的切线,
∴∠OFP=90°=∠PCO,
∴P、F、O、C四点共圆,
∴∠1=∠2,
∴∠DOE=∠AFC,且∠D=∠A,
∴△DOE∽△AFC,
∴
| DE |
| AC |
| OD |
| AF |
| 2OD |
| 2AF |
| CD |
| AB |
又∵∠A=∠D,
∴△DCE∽△ABC,
∴∠DCE=∠ABC,
∴∠ACE=∠3+∠DCE=∠4+∠ABC=∠DBC=90°,
∴AC⊥CE.
点评:本题考查了切线的性质,等腰三角形的性质和判定,三角形内角和定理的应用,解此题的关键是能正确作出辅助线,得出∠ACE=∠DBC,题目比较好,难度适中.

练习册系列答案
相关题目
下列各对数中,数值相等的是( )
| A、-32与-23 |
| B、(-3)2与-32 |
| C、-23与(-2)3 |
| D、(-3×2)3与-3×23 |
几个棱长为1的小正方体组成的几何体,从正面、左面、上面看到的形状图如图所示,则这个几何体的表面积为( )


| A、7 | B、11 | C、14 | D、22 |
 如图:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的高为
如图:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的高为