题目内容
 如图:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的高为
如图:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的高为考点:等边三角形的性质
专题:规律型
分析:根据等边三角形的性质和∠MON=30°,可求得∠OB1A2=90°,可求得A1A2=2OA1=2,同理可求得OAn+1=2OAn=4OAn-1=…=2n-1OA2=2nOA1=2n,再结合含30°角的直角三角形的性质可求得△AnBnAn+1的边长,进一步可求得面积,可得出答案.
解答:解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠MON=30°,
∴∠OB1A2=90°,可求得A1A2=2OA1=2,
同理可求得OAn+1=2OAn=4OAn-1=…=2n-1OA2=2nOA1=2n,
在△OBnAn+1中,∠O=30°,∠BnAn+1O=60°,
∴∠OBnAn+1=90°,
∴BnAn+1=
OAn+1=
×2n=2n-1,
即△AnBnAn+1的边长为2n-1,则可求得其高为
×2n-1=
×2n-2,
∴△A6B6A7的高为
×26-2=16
,△AnBnAn+1的面积为
×(2n-1)2=
×22n-4,
故答案为:16
;
×22n-4.
∴∠B1A1A2=60°,
∵∠MON=30°,
∴∠OB1A2=90°,可求得A1A2=2OA1=2,
同理可求得OAn+1=2OAn=4OAn-1=…=2n-1OA2=2nOA1=2n,
在△OBnAn+1中,∠O=30°,∠BnAn+1O=60°,
∴∠OBnAn+1=90°,
∴BnAn+1=
| 1 |
| 2 |
| 1 |
| 2 |
即△AnBnAn+1的边长为2n-1,则可求得其高为
| ||
| 2 |
| 3 |
∴△A6B6A7的高为
| 3 |
| 3 |
| ||
| 4 |
| 3 |
故答案为:16
| 3 |
| 3 |
点评:本题主要考查等边三角形的性质和含30°角的直角三角形的性质,根据条件找到等边三角形的边长和OA1的关系是解题的关键,注意等边三角形的面积公式为S=
a2(a为等边三角形的边长).
| ||
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
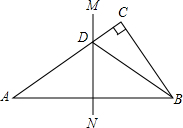 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )
如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )| A、4cm | B、5cm |
| C、6cm | D、7cm |
埃(āi)是光波长度和分子直径的常用计量单位.1埃为一百亿分之一米,其中,一百亿分之一米用科学记数法可表示为( )
| A、1×10-9米 |
| B、1×10-10米 |
| C、0.1×-910米 |
| D、10×10-10米 |
下列各组中两项属于同类项的是( )
| A、-x2y和2xy2 |
| B、2x2y与-x2yz |
| C、3m3n和-nm3 |
| D、2n2m与-2m2n |
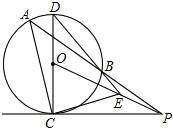 如图,PAB为⊙O的割线,PC切⊙O于C,CD为⊙O的直径,DB交PO于E.求证:AC⊥CE.
如图,PAB为⊙O的割线,PC切⊙O于C,CD为⊙O的直径,DB交PO于E.求证:AC⊥CE. 如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.
如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.