题目内容
我们可以在面积为3×4的矩形中画出多种棱长为1的正方体的表面展开图.
(1)请你设计一种面积比3×4更小的矩形,使得我们能在其中画出棱长为1的正方体的表面展开图,并画出这个正方体的表面展开图.
(2)如果给你同样的面积为3×4的矩形,请你在其中画出棱长大于1的正方体的表面展开图,并计算你所画正方体的表面展开图折成正方体后的棱长.
(1)请你设计一种面积比3×4更小的矩形,使得我们能在其中画出棱长为1的正方体的表面展开图,并画出这个正方体的表面展开图.
(2)如果给你同样的面积为3×4的矩形,请你在其中画出棱长大于1的正方体的表面展开图,并计算你所画正方体的表面展开图折成正方体后的棱长.
考点:几何体的展开图
专题:
分析:(1)画出“33”结构的正方体展开图即可;
(2)由于要画出棱长大于1的正方体的表面展开图,则将展开图倾斜放在面积为3×4的矩形中,再根据相似三角形的性质和勾股定理即可求解.
(2)由于要画出棱长大于1的正方体的表面展开图,则将展开图倾斜放在面积为3×4的矩形中,再根据相似三角形的性质和勾股定理即可求解.
解答:解:(1)如图所示:

(2)如图所示:

设AF=x,则BE=4x,AE=3-4x,BG=4-x,
∵∠AEF+∠AFE=∠AEF+∠BEG=90°,
∴∠AFE=∠BEG,
∵∠A=∠B,
△AFE∽△BEG,
∴(3-4x):(4-x)=1:4,
解得x=
,
AE=3-4x=
,
在Rt△AEF中,EF=
=
.
故正方体的表面展开图折成正方体后的棱长是
.

(2)如图所示:

设AF=x,则BE=4x,AE=3-4x,BG=4-x,
∵∠AEF+∠AFE=∠AEF+∠BEG=90°,
∴∠AFE=∠BEG,
∵∠A=∠B,
△AFE∽△BEG,
∴(3-4x):(4-x)=1:4,
解得x=
| 8 |
| 15 |
AE=3-4x=
| 13 |
| 15 |
在Rt△AEF中,EF=
(
|
| ||
| 15 |
故正方体的表面展开图折成正方体后的棱长是
| ||
| 15 |
点评:主要考查了正方体的表面展开图.正方体的表面展开图的各种形式归类为“1,4,1”6种,“1,3,2”3种,“3,3”1种,“2,2,2”1种,共有11种.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
埃(āi)是光波长度和分子直径的常用计量单位.1埃为一百亿分之一米,其中,一百亿分之一米用科学记数法可表示为( )
| A、1×10-9米 |
| B、1×10-10米 |
| C、0.1×-910米 |
| D、10×10-10米 |
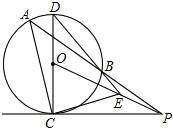 如图,PAB为⊙O的割线,PC切⊙O于C,CD为⊙O的直径,DB交PO于E.求证:AC⊥CE.
如图,PAB为⊙O的割线,PC切⊙O于C,CD为⊙O的直径,DB交PO于E.求证:AC⊥CE.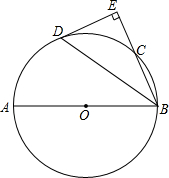 如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC交BC的延长线于点E.
如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC交BC的延长线于点E. 如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)
如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)