题目内容
8.已知(a-1)2+|2b-3|+(c+1)2=0,求$\frac{ab}{3c}$-$\frac{a-c}{b}$的值.分析 根据非负数的性质列式求出a、b、c的值,然后代入代数式进行计算即可得解.
解答 解:由非负数性质可得$\left\{\begin{array}{l}{a-1=0}\\{2b-3=0}\\{c+1=0}\end{array}\right.$,
解得:a=1,b=$\frac{3}{2}$,c=-1,
∴$\frac{ab}{3c}$-$\frac{a-c}{b}$=$\frac{1×\frac{3}{2}}{3×(-1)}$-$\frac{1-(-1)}{\frac{3}{2}}$
=-$\frac{1}{2}$-$\frac{4}{3}$
=-$\frac{11}{6}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
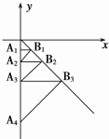 如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,再过点A2作y轴的垂线,交直线y=-x于点B2…则点B4的坐标为($\frac{8}{3}$,-$\frac{8}{3}$).
如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,再过点A2作y轴的垂线,交直线y=-x于点B2…则点B4的坐标为($\frac{8}{3}$,-$\frac{8}{3}$). 如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P.若存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等,则点Q的坐标为(6,2$\sqrt{21}$)或(6,3)或(10,12)或(4+$\sqrt{14}$,6+$\sqrt{14}$)或(4-$\sqrt{14}$,6-$\sqrt{14}$).
如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P.若存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等,则点Q的坐标为(6,2$\sqrt{21}$)或(6,3)或(10,12)或(4+$\sqrt{14}$,6+$\sqrt{14}$)或(4-$\sqrt{14}$,6-$\sqrt{14}$).