题目内容

13．利用分解因式计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{{10}^{2}}$）

分析 利用平方差公式逐一分解，再进一步计算约分抵消得出答案即可．

解答 解：原式=（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1-$\frac{1}{3}$）（1+$\frac{1}{3}$）（1-$\frac{1}{4}$）（1+$\frac{1}{4}$）…（1-$\frac{1}{10}$）（1+$\frac{1}{10}$）
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{9}{10}$×$\frac{11}{10}$
=$\frac{11}{20}$．

点评 此题考查因式分解的实际运用，掌握平方差公式是解决问题的关键．

练习册系列答案
相关题目
3．挂钟的分针长10cm，经过45min，它的针尖转过的路程是（　　）
A．15πcmB．75πcmC．$\frac{75π}{2}$cmD．$\frac{15π}{2}cm$
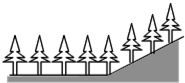4．如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）为4m．如果在坡比为i=1：$\frac{4}{3}$的山坡上种树，也要求株距为4m，那么相邻两树间的坡面距离为（　　）
A．5mB．6mC．7mD．8m
1．化简：2a-[-3b-3（3a-b）]．
8．已知4x2+y2-4x-6y+10=0，求（$\frac{2}{3}$x$\sqrt{9x}$+y2$\sqrt{\frac{x}{{y}^{2}}}$）-（x2$\sqrt{\frac{1}{x}}$-5x$\sqrt{\frac{y}{x}}$）的值．
18．解方程：64（x+1）3=343．
5．正方形的边长为10cm，在其中挖去一个边长为x cm的正方形
（1）求x的取值范围；
（2）若剩余部分的面积为y cm2，写出y与x的函数解析式；
（3）当挖去的正方形的边长为1cm、2cm、3cm、$\sqrt{70}$cm时，求剩余部分的面积．
2．用不等式表示下列数量关系：
（1）a与1的和是正数a+1＞0；
（2）a的$\frac{1}{2}$和b的$\frac{1}{3}$的差是负数$\frac{1}{2}a$-$\frac{1}{3}b$＜0；
（3）a与b的两数和的平方不大于9（a+b）2≤9；
（4）a的$\frac{3}{2}$倍与b的和的平方是非负数（$\frac{3}{2}$a+b）2≥0．
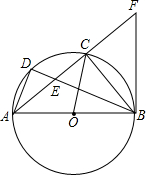19．如图，在△ABC内接于⊙O，AB为直径，D是$\widehat{AC}$上的点，BD交AC于点E，过点B作⊙O的切线与AC的延长线交于点F，已知AB=5，sin∠CAB=$\frac{3}{5}$．
（1）求CF的长；
（2）若CE=$\frac{9}{4}$，求证：AD∥OC；
（3）在满足（2）的条件下，求AD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网