题目内容
15.已知△ABC中,AB=4,AC=6,D是AB的中点,E为AC边上的点,△ADE与△ABC相似,则AE=3或$\frac{4}{3}$.分析 分类讨论:当△ADE∽△ABC时,$\frac{AE}{AC}$=$\frac{AB}{AD}$,即$\frac{AE}{6}$=$\frac{2}{4}$;当△ADE∽△ACB时,$\frac{AE}{AB}$=$\frac{AD}{AC}$,即$\frac{AE}{4}$=$\frac{2}{6}$,然后根据比例性质分别计算出对应的AE的值.
解答 解:当△ADE∽△ABC时,$\frac{AE}{AC}$=$\frac{AB}{AD}$,即$\frac{AE}{6}$=$\frac{2}{4}$,则AE=3;
当△ADE∽△ACB时,$\frac{AE}{AB}$=$\frac{AD}{AC}$,即$\frac{AE}{4}$=$\frac{2}{6}$,则AE=$\frac{4}{3}$,
所以AE的长为3或$\frac{4}{3}$.
故答案为:3或$\frac{4}{3}$.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5. 将一个小球在如图所示的地砖上自由滚动,最终没有停在黑色方砖上的概率为( )
将一个小球在如图所示的地砖上自由滚动,最终没有停在黑色方砖上的概率为( )
 将一个小球在如图所示的地砖上自由滚动,最终没有停在黑色方砖上的概率为( )
将一个小球在如图所示的地砖上自由滚动,最终没有停在黑色方砖上的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
6.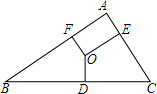 如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( )
如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( )
 如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( )
如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( )| A. | a:b:c | B. | $\frac{1}{a}$:$\frac{1}{b}$:$\frac{1}{c}$ | C. | sinA:sinB:sinC | D. | cosA:cosB:cosC |
3.挂钟的分针长10cm,经过45min,它的针尖转过的路程是( )
| A. | 15πcm | B. | 75πcm | C. | $\frac{75π}{2}$cm | D. | $\frac{15π}{2}cm$ |
10.设抛物线y=x2-4x+k的顶点在直线y=x上,则k的值为( )
| A. | -6 | B. | -4 | C. | 4 | D. | 6 |
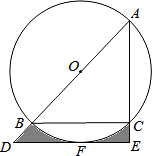 如图,已知:AB为⊙O的直径,C为⊙O上一点,F为$\widehat{BC}$的中点,过F作DE∥BC交AB的延长线于D,交AC的延长线于E.
如图,已知:AB为⊙O的直径,C为⊙O上一点,F为$\widehat{BC}$的中点,过F作DE∥BC交AB的延长线于D,交AC的延长线于E.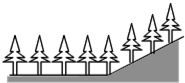 如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡比为i=1:$\frac{4}{3}$的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( )
如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡比为i=1:$\frac{4}{3}$的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( )