题目内容
15.如图,在圆周上两个不同的点上分别写上1,2,第1次操作:在数字1、2将圆周分成的两条圆弧中点上写上$\frac{1+2}{1}$=3,第2次操作:在数字1,3,2,3将圆周分成的四条圆弧中点依次写上$\frac{1+3}{2}$=2,$\frac{3+2}{2}$=$\frac{5}{2}$,$\frac{2+3}{2}$=$\frac{5}{2}$,$\frac{3+1}{2}$=2,…,第k次操作是在上一次操作基础上,在每两个相邻的数分成的圆弧中点写上这两个数和的$\frac{1}{k}$(k≠0),第2016次操作后圆周上所有数字的和与第2015次操作后圆周上所有数字的和的比是$\frac{1009}{1008}$.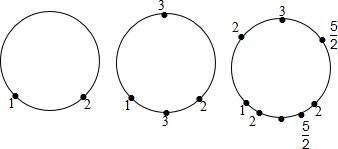
分析 设第n次操作后圆周上所有数字的和为an,数字的个数为x个,根据写数的规律可知an+1=$\frac{n+3}{n+1}{a}_{n}$,根据该规律即可解决问题.
解答 解:设第n次操作后圆周上所有数字的和为an,数字的个数为x个,
根据写数的规律可知,第n个图形上的每个数字用到2次,
∴an+1=an+$\frac{2}{n+1}$an=$\frac{n+3}{n+1}{a}_{n}$.
令n=2015,则有a2016=$\frac{2018}{2016}$a2015.
∴$\frac{{a}_{2016}}{{a}_{2015}}$=$\frac{2018}{2016}$=$\frac{1009}{1008}$.
故答案为:$\frac{1009}{1008}$.
点评 本题考查了规律型的数字的变化以及图形的变化,解题的关键是找出规律“an+1=$\frac{n+3}{n+1}{a}_{n}$”.本题属于基础题,难度不大,解决该题型题目时,结合图形与数字的变化找出变化规律是关键.

练习册系列答案
相关题目
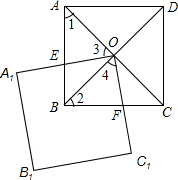 如图,正方形ABCD的面积为4,对角线交于点O,点O是正方形A1B1C1O的一个顶点,如果这两个正方形全等,正方形A1B1C1O绕点O旋转.
如图,正方形ABCD的面积为4,对角线交于点O,点O是正方形A1B1C1O的一个顶点,如果这两个正方形全等,正方形A1B1C1O绕点O旋转.