Question

9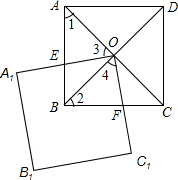．如图，正方形ABCD的面积为4，对角线交于点O，点O是正方形A₁B₁C₁O的一个顶点，如果这两个正方形全等，正方形A₁B₁C₁O绕点O旋转．
（1）求两个正方形重叠部分的面积；
（2）若正方形A₁B₁C₁O旋转到B₁在DB的延长线时，求A与C₁的距离．

Answer 1

分析 （1）先判断出△AOE≌△BOF（ASA），然后得到S_△AOE=S_△BOF，再说明S_{两个正方形重叠部分}=S_ABO=$\frac{1}{4}$S_{正方形ABCD}即可；
（2）先C₁F=$\frac{1}{2}$OC₁=1，AG=1，再利用勾股定理即可．

解答 解：（1）∵四边形ABCD为正方形，
∴∠OAB=∠OBF=45°，OA=OB
∵BO⊥AC，
∴∠AOE+∠EOB=90°，
又∵四边形A₁B₁C₁O为正方形，
∴∠A₁OC₁=90°，即∠BOF+∠EOB=90°，
∴∠AOE=∠BOF，
在△AOE和△BOF中，
$\left\{\begin{array}{l}{∠AOE=∠BOF}\\{AO=BO}\\{∠OAE=∠OBF}\end{array}\right.$，
∴△AOE≌△BOF（ASA），
∵S_{两个正方形重叠部分}=S_△BOE+S_△BOF，
又S_△AOE=S_△BOF
∴S_{两个正方形重叠部分}=S_ABO=$\frac{1}{4}$S_{正方形ABCD}=$\frac{1}{4}$×4=1；
（2）如图，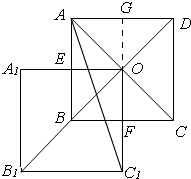

∵正方形的面积为4，
∴AD=AB=2，
∵正方形A₁B₁C₁O旋转到B₁在DB的延长线时，
∴C₁F=$\frac{1}{2}$OC₁=1，AG=1
∴C₁G=3，
根据勾股定理，得AC₁=$\sqrt{10}$．

点评 此题是旋转性质题，主要考查了正方形的性质，勾股定理，解本题的关键是熟练运用正方形的性质．