已知x=$\frac{\sqrt{5}-1}{2}$.y=$\frac{\sqrt{5}+1}{2}$.求x2+xy+y2的值．题目和参考答案——青夏教育精英家教网—

题目内容

8．已知x=$\frac{\sqrt{5}-1}{2}$，y=$\frac{\sqrt{5}+1}{2}$，求x²+xy+y²的值．

分析根据题意求出x+y和xy的值，根据完全平方公式把原式变形，代入计算即可．

解答解：∵x=$\frac{\sqrt{5}-1}{2}$，y=$\frac{\sqrt{5}+1}{2}$，
∴x+y=$\sqrt{5}$，xy=$\frac{\sqrt{5}-1}{2}$×$\frac{\sqrt{5}+1}{2}$=1，
则x²+xy+y²=x²+2xy+y²-xy=（x+y）²-xy=5-1=4

点评本题考查的是二次根式的化简求值，掌握合并同类二次根式的法则、正确运用完全平方公式是解题的关键．

练习册系列答案

15．如图，在圆周上两个不同的点上分别写上1，2，第1次操作：在数字1、2将圆周分成的两条圆弧中点上写上$\frac{1+2}{1}$=3，第2次操作：在数字1，3，2，3将圆周分成的四条圆弧中点依次写上$\frac{1+3}{2}$=2，$\frac{3+2}{2}$=$\frac{5}{2}$，$\frac{2+3}{2}$=$\frac{5}{2}$，$\frac{3+1}{2}$=2，…，第k次操作是在上一次操作基础上，在每两个相邻的数分成的圆弧中点写上这两个数和的$\frac{1}{k}$（k≠0），第2016次操作后圆周上所有数字的和与第2015次操作后圆周上所有数字的和的比是$\frac{1009}{1008}$．

16．

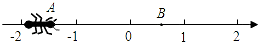如图，一只蚂蚁从点A沿数轴向右直爬2个单位到达点B，点A表示-$\sqrt{2}$，设点B所表示的数为m，则（m-1）（m-3）的值为1．

3．

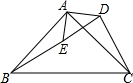如图，△ABC是等腰直角三角形，∠BAC=90°，△ADC绕点A旋转，使得边AC与AB重合，点D与点E重合，若AD=3，则DE=3$\sqrt{2}$．

13．已知当x=1与x=-4时，代数式x²+bx+c的值都是8，求b、c的值．

20．当x=1时，代数式ax³+bx+1的值是2，则方程$\frac{ax+1}{2}$+$\frac{2bx-3}{4}$=$\frac{x}{4}$的解是（　　）

17．先化简，后求值：（a-b）•（b+a）-（a-b）²，其中a=-2，b=3．

18．计算-4x⁵÷2x³的结果等于-2x²．

试题分类