题目内容
9.O是△ABC内一点,且到三边的距离相等,若∠A=56°,则∠BOC=118°.分析 根据O到三角形三边距离相等,得到O是内心,再利用三角形内角和定理和角平分线的概念即可求出∠BOC的度数.
解答 解:∵O到三角形三边距离相等,
∴O是内心,
∴AO,BO,CO都是角平分线,
∴∠CBO=∠ABO=$\frac{1}{2}$∠ABC,∠BCO=∠ACO=$\frac{1}{2}$∠ACB,
∠ABC+∠ACB=180°-56°=124°,
∠OBC+∠OCB=62°,
∠BOC=180°-62°=118°.
故答案为:118.
点评 本题考查的是角平分线的定义和三角形的内心的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.对于实数a、b,规定a⊕b=a-2b,若4⊕(x-3)=2,则x的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{5}{2}$ | D. | 4 |
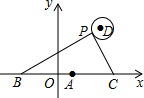 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
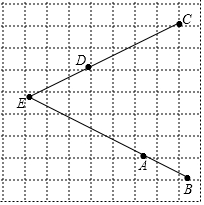 如图,在每个小正方形的边长为1的网格中,A,B为小正方形边的中点,C,D为格点,E为BA,CD的延长线的交点.
如图,在每个小正方形的边长为1的网格中,A,B为小正方形边的中点,C,D为格点,E为BA,CD的延长线的交点. (1)如图,请用尺规作图法,确定出图中残缺的圆形铁片的圆心.
(1)如图,请用尺规作图法,确定出图中残缺的圆形铁片的圆心.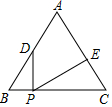 如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个.
如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个.