题目内容
17.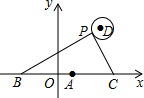 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 首先证明AB=AC=a,根据条件可知PA=AB=AC=a,求出⊙D上到点A的最大距离即可解决问题.
解答 解: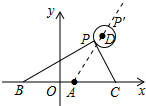 ∵A(1,0),B(1-a,0),C(1+a,0)(a>0),
∵A(1,0),B(1-a,0),C(1+a,0)(a>0),
∴AB=1-(1-a)=a,CA=a+1-1=a,
∴AB=AC,
∵∠BPC=90°,
∴PA=AB=AC=a,
如图延长AD交⊙D于P′,此时AP′最大,
∵A(1,0),D(4,4),
∴AD=5,
∴AP′=5+1=6,
∴a的最大值为6.
故选D.
点评 本题考查圆、最值问题、直角三角形性质等知识,解题的关键是发现PA=AB=AC=a,求出点P到点A的最大距离即可解决问题,属于中考常考题型.

练习册系列答案
相关题目
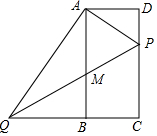 如图,在矩形ABCD中,点P在边CD上,与点C、D不重合,过点A作AP的垂线与CB的延长线交于点Q,连接PQ,M为线段PQ中点
如图,在矩形ABCD中,点P在边CD上,与点C、D不重合,过点A作AP的垂线与CB的延长线交于点Q,连接PQ,M为线段PQ中点