题目内容
4．分式$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$的最小值是4．分析 首先将分式变形为6-$\frac{2}{（x+1）^{2}+1}$，依据代数式可知当x=-1时，分式有最小值．
解答 解：$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$=$\frac{6{x}^{2}+12x+12-2}{{x}^{2}+2x+2}$=6-$\frac{2}{{x}^{2}+2x+2}$=6-$\frac{2}{（x+1）^{2}+1}$．
∴当x=-1时，分式$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$有最小值，分式的最小值=6-2=4．
故答案为：4．
点评 本题主要考查的是二次函数的最值问题，能够将分式进行适当变形是解题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
14．已知x＞2，则下列变形正确的是（ ）
| A． | -x＜2 | B． | 若y＞2，则x-y＞0 | C． | -$\frac{1}{2}$x+2＜1 | D． | 若y＞2，则$\frac{x}{y}＞1$ |
16．一个两位数，十位上的数字是x，个位上的数字是y，把这个两位数十位上数字与个位上数字调换位置后的两位数用代数式表示为（ ）
| A． | yx | B． | xy | C． | 10y+x | D． | 10x+y |
小明在荡秋千时，发观秋千在静止时，秋千离地面3dm（EF=3dm），荡起的水平距离为13dm（BC=13dm）时，离地面8dm（BD=8dm），求秋千的绳索AF的长．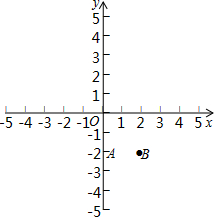
在如图的平面直角坐标系xOy中，抛物线y=2x2+bx+c经过点A（0，-2），B（2，-2）．