题目内容
15.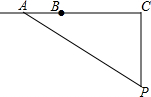 如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.
如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.(1)求A、B两点间的距离;
(2)试说明该车是否超过限速.
分析 (1)由三角函数求出AC,证出△BCP是等腰直角三角形,得出BC=PC=60米,求出AB=AC-BC=20米即可;
(2)求出该车从点A行驶到点B的速度为20米/秒=72千米/小时<80千米/小时,即可得出结果.
解答 解:如图所示: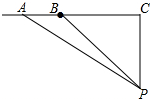
(1)∵PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$=$\frac{AC}{PC}$,
∴AC=80米,
∵∠BPC=45°,
∴△BCP是等腰直角三角形,
∴BC=PC=60米,
∴AB=AC-BC=20米,
答:A、B两点间的距离为20米;
(2)该车不超过限速;理由如下:
由题意得:该车从点A行驶到点B所用时间为1秒,
∴该车从点A行驶到点B的速度为20米/秒=72千米/小时<80千米/小时,
∴该车不超过限速.
点评 本题考查了解直角三角形的应用、等腰直角三角形的判定与性质;熟练掌握解直角三角形,由三角函数求出AC是解决问题(1)的关键.

练习册系列答案
相关题目
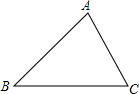 如图,已知△ABC中,AC=6,∠ABC=45°.
如图,已知△ABC中,AC=6,∠ABC=45°. 如图,⊙O是△ABC外接圆,∠A=45°,BD为⊙O的直径,BD=2,连结CD,求BC的长$\sqrt{2}$.
如图,⊙O是△ABC外接圆,∠A=45°,BD为⊙O的直径,BD=2,连结CD,求BC的长$\sqrt{2}$. 已知∠BOC=30°,OM平分∠AOC,ON平分∠BOC,
已知∠BOC=30°,OM平分∠AOC,ON平分∠BOC, 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A(-2,m),B(5,-2)两点,与x轴交于C点,过A作AD⊥x轴于D.
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A(-2,m),B(5,-2)两点,与x轴交于C点,过A作AD⊥x轴于D.