题目内容
5.化简求值:(1)$\frac{3x-3}{{x}^{2}-1}÷\frac{3x}{x+1}-\frac{1}{x-1}$,其中x=2.
(2)先化简$\frac{2a+2}{a-1}$÷(a+1)+$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$,然后在-1,1,2中选一恰当值代入求值.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把x=2代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选出合适的a的值代入进行计算即可.
解答 解:(1)原式=$\frac{3}{x+1}$•$\frac{x+1}{3x}$-$\frac{1}{x-1}$
=$\frac{1}{x}$-$\frac{1}{x-1}$
=$\frac{x-1-x}{x(x-1)}$
=-$\frac{1}{x(x-1)}$,
当x=2时,原式=-$\frac{1}{2(2-1)}$=-$\frac{1}{2}$;
(2)原式=$\frac{2(a+1)}{a-1}$•$\frac{1}{a+1}$+$\frac{a+1}{a-1}$
=$\frac{2}{a-1}$+$\frac{a+1}{a-1}$
=$\frac{a+3}{a-1}$.
当a=2时,原式=5.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
17. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=20,则AB的长是( )
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=20,则AB的长是( )
 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=20,则AB的长是( )
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=20,则AB的长是( )| A. | 9$\sqrt{2}$ | B. | $\frac{90}{7}$ | C. | 13 | D. | 16 |
 往返于A、B两个城市的客车,中途有C、D、E三个停靠点
往返于A、B两个城市的客车,中途有C、D、E三个停靠点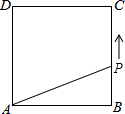 如图,在边长为$\sqrt{2}$的正方形ABCD的一边BC上,有一点P从B点运动到C点,设PB=x,四边形APCD的面积为y.写出y与x之间的关系式为y=-$\frac{\sqrt{2}}{2}$x+2(0≤x<$\sqrt{2}$)(要写出自变量的取值范围).
如图,在边长为$\sqrt{2}$的正方形ABCD的一边BC上,有一点P从B点运动到C点,设PB=x,四边形APCD的面积为y.写出y与x之间的关系式为y=-$\frac{\sqrt{2}}{2}$x+2(0≤x<$\sqrt{2}$)(要写出自变量的取值范围). 如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.
如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.