题目内容
3.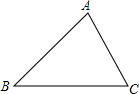 如图,已知△ABC中,AC=6,∠ABC=45°.
如图,已知△ABC中,AC=6,∠ABC=45°.(1)用直尺和圆规作出△ABC的外接圆(保留作图痕迹,写出结论,不写画法);
(2)求出△ABC的外接圆半径.
分析 (1)作AB和BC的垂直平分线,它们相交于点O,然后以O为圆心,OA为半径作⊙O即可;
(2)连结OC、OA,如图,根据圆周角定理得到∠AOC=2∠ABC=90°,则可判断△OAC为等腰直角三角形,然后根据等腰直角三角形的性质求出OA即可.
解答 解:(1)如图,⊙O为所作;
(2)连结OC、OA,如图,
∵∠AOC=2∠ABC=90°,
而OA=OC,
∴△OAC为等腰直角三角形,
∴OA=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$×6=3$\sqrt{2}$,
即△ABC的外接圆半径为3$\sqrt{2}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形的外心.

练习册系列答案
相关题目
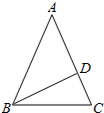 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论中:
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论中: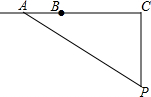 如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.
如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.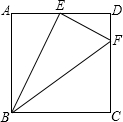 在正方形ABCD中,点E为AD中点,DF=$\frac{1}{4}$CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为$\frac{1}{2}$AB;(4)$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$.其中正确的有( )
在正方形ABCD中,点E为AD中点,DF=$\frac{1}{4}$CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为$\frac{1}{2}$AB;(4)$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$.其中正确的有( )