题目内容
7．
如图，⊙O是△ABC外接圆，∠A=45°，BD为⊙O的直径，BD=2，连结CD，求BC的长$\sqrt{2}$．
分析 连接OC，根据圆周角定理得到∠BOC=90°，根据等腰直角三角形的性质计算即可．
解答 解：
连接OC，
∠BOC=2∠A=90°，
∵BD=2，
∴OB=OC=1，
又∵∠BOC=90°，
∴BC=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查的是圆周角定理和等腰直角三角形的性质，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
17．
如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，$\widehat{AC}$，$\widehat{BC}$的中点分别是M，N，P，Q．若MP+NQ=14，AC+BC=20，则AB的长是（ ）
如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，$\widehat{AC}$，$\widehat{BC}$的中点分别是M，N，P，Q．若MP+NQ=14，AC+BC=20，则AB的长是（ ）| A． | 9$\sqrt{2}$ | B． | $\frac{90}{7}$ | C． | 13 | D． | 16 |
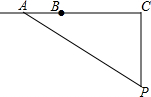如图，l为一条东西方向的笔直公路，一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶，依次经过点A、B、C，P是一个观测点，PC⊥l，PC=60米，tan∠APC=$\frac{4}{3}$，∠BPC=45°，测得该车从点A行驶到点B所用时间为1秒．
如图，已知O是坐标原点，A、B的坐标分别为（3，1），（2，-1）．
如图，点G为△ABC的重心，DE经过点G，DE∥AC，EF∥AB，如果DE的长是4，那么CF的长是2．