题目内容
18. 如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.
如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.
分析 根据折叠的性质得到∠AEC=∠AED,根据垂直的定义得到∠BED=90°,根据平角的定义得到∠AEB=45°,推出△ABE是等腰直角三角形,于是得到结论.
解答 解:∵将AC沿AE折叠,使点C与点D重合,
∴∠AEC=∠AED,
∵DE⊥BC,
∴∠BED=90°,
∴∠AEC=90°+∠AEB,
∵∠AEC+∠AEB=180°,
∴∠AEB+90°+∠AEB=180°,
∴∠AEB=45°,
∵∠B=90°,
∴△ABE是等腰直角三角形,
∴AE=$\sqrt{2}$AB=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题考查了翻折变换-折叠问题,等腰直角三角形的判定和性质,正确的理解题意是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
20.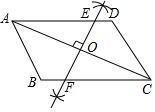 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,
(1)作图:作AC的垂直平分线,分别交AD、BC、AC于点E、F、O(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求证:△AOE≌△COF.
 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,(1)作图:作AC的垂直平分线,分别交AD、BC、AC于点E、F、O(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求证:△AOE≌△COF.
13.如果a、b、c是一个直角三角形的三边,则a:b:c可以等于( )
| A. | 1:2:4 | B. | 2:3:4 | C. | 3:4:7 | D. | 5:12:13 |
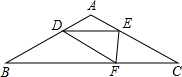 如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.
如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.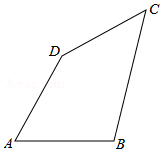 如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.


