题目内容
9.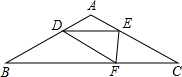 如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.
如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.
分析 由于在△ABC中,AB=AC,AD=AE,可得DE∥BC,根据等腰三角形的性质和平行线的性质可得∠EDF=30°,再根据含30度角的直角三角形的性质以及勾股定理,分∠DFE=90°和∠DEF=90°两种情况讨论可求AD的长.
解答 解:∵在△ABC中,AB=AC,AD=AE,
∴DE∥BC,
∵∠B=30°,
∴∠EDF=30°,
∴当∠DFE=90°时,设AD=x,则BD=DF=15-x,DE=$\sqrt{3}$x,则15-x=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$x,解得x=6;
当∠DEF=90°时,设AD=x,则BD=DF=15-x,DE=$\sqrt{3}$x,则$\frac{\sqrt{3}}{2}$×(15-x)=$\sqrt{3}$x,解得x=5.
综上所述,AD=5或6.
故答案为:5或6.
点评 本题考查了勾股定理,等腰三角形的性质和平行线的判定和性质,含30度角的直角三角形的性质,以及分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
相关题目
11. 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | $\sqrt{11}$ | D. | $\sqrt{17}$ |
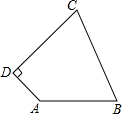 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.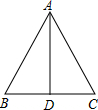 等腰三角形的腰长为13,底为10.求它的面积.
等腰三角形的腰长为13,底为10.求它的面积. 如图,在四边形ABCD中,AD=DC,DF是∠ADC的平分线,AF∥BC,连接AC,CF.求证:CA是∠BCF的平分线.
如图,在四边形ABCD中,AD=DC,DF是∠ADC的平分线,AF∥BC,连接AC,CF.求证:CA是∠BCF的平分线. 如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.
如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.