题目内容
20.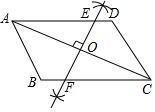 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,(1)作图:作AC的垂直平分线,分别交AD、BC、AC于点E、F、O(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求证:△AOE≌△COF.
分析 (1)根据线段垂直平分线的作法作出AC的垂直平分线DF即可;
(2)先根据平行线的性质得出∠EAO=∠FCO,再由ASA定理即可得出结论.
解答  解:(1)如图,DF即为线段AC的垂直平分线;
解:(1)如图,DF即为线段AC的垂直平分线;
(2)∵AD∥BC,
∴∠EAO=∠FCO.
在△AOE与COF中,
∵$\left\{\begin{array}{l}{∠AOE=∠COF}\\{OA=OC}\\{∠EAO=∠FCO}\end{array}\right.$,
∴△AOE≌△COF(ASA).
点评 本题考查的是作图-基本作图及全等三角形的判定定理,熟知线段垂直平分线的作法是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.双曲线y=$\frac{1-k}{x}$与直线y=x没有交点,则k的取值范围是( )
| A. | k<1 | B. | k>1 | C. | k<-1 | D. | k>-1 |
11. 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | $\sqrt{11}$ | D. | $\sqrt{17}$ |
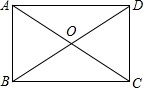 如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.
如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.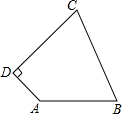 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积. 如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.
如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.