题目内容
8.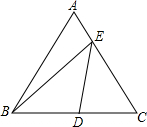 如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
分析 作B关于AC的对称点B′,连接BB′、B′D,交AC于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D就是BE+ED的最小值,故E即为所求的点.
解答 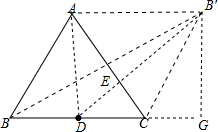 解:作B关于AC的对称点B′,连接BB′、B′D,交AC于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D就是BE+ED的最小值,
解:作B关于AC的对称点B′,连接BB′、B′D,交AC于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D就是BE+ED的最小值,
∵B、B′关于AC的对称,
∴AC、BB′互相垂直平分,
∴四边形ABCB′是平行四边形,
∵三角形ABC是边长为2,
∵D为BC的中点,
∴AD⊥BC,
∴AD=$\sqrt{3}$,BD=CD=1,BB′=2AD=2$\sqrt{3}$,
作B′G⊥BC的延长线于G,
∴B′G=AD=$\sqrt{3}$,
在Rt△B′BG中,
BG=$\sqrt{BB{′}^{2}-B′{G}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3,
∴DG=BG-BD=3-1=2,
在Rt△B′DG中,B′D=$\sqrt{D{G}^{2}+B′{G}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$.
故BE+ED的最小值为$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查的是最短路线问题,涉及的知识点有:轴对称的性质、等边三角形的性质、勾股定理等,有一定的综合性,但难易适中.

练习册系列答案
相关题目
13.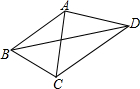 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )| A. | 68° | B. | 88° | C. | 90° | D. | 112° |
20.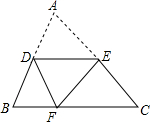 如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
 如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )| A. | 65° | B. | 50° | C. | 60° | D. | 57.5° |
18. 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )
 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )| A. | 正方体 | B. | 长方体 | C. | 三棱柱 | D. | 三棱锥 |
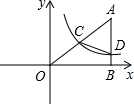 如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D.
如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D. 如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有8个.
如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有8个. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为$\widehat{BD}$的中点.若∠A=40°,则∠B=70度.
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为$\widehat{BD}$的中点.若∠A=40°,则∠B=70度.