题目内容
3.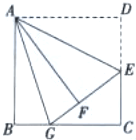 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.(1)求证:△ABG≌△AFG;
(2)求BG的长.
分析 (1)利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;
(2)利用勾股定理得出GE2=CG2+CE2,进而求出BG即可;
解答 解:(1)在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
$\left\{\begin{array}{l}{AG=AG}\\{AB=AF}\end{array}\right.$,
∴△ABG≌△AFG(HL);
(2)∵△ABG≌△AFG,
∴BG=FG,
设BG=FG=x,则GC=6-x,
∵E为CD的中点,
∴CE=EF=DE=3,
∴EG=3+x,
∴在Rt△CEG中,32+(6-x)2=(3+x)2,解得x=2,
∴BG=2.
点评 此题主要考查了勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.

练习册系列答案
相关题目
13.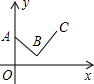 如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )
如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )
 如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )
如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{3}$ |


 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: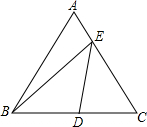 如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
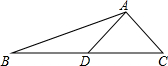 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求: