题目内容
20.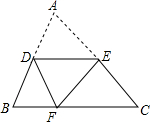 如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )| A. | 65° | B. | 50° | C. | 60° | D. | 57.5° |
分析 先根据图形翻折不变性的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算即可求解.
解答 解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=65°,
∴∠BDF=180°-∠B-∠BFD=180°-65°-65°=50°.
故选:B.
点评 本题考查的是图形翻折变换的图形能够重合的性质,以及等边对等角的性质,熟知折叠的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.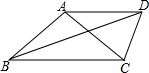 如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
 如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
5. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
10.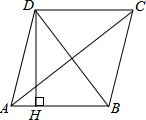 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 12 | D. | 24 |
 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: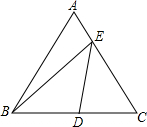 如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为$\sqrt{7}$.
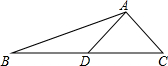 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求: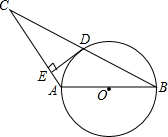 如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.